
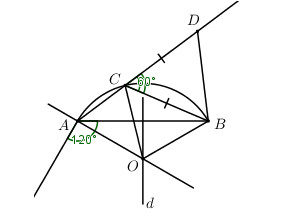
Cho dây AB chắn một cung có số đo là \({120^o}\) trên đường tròn (O). Một điểm C di động trên cung lớn AB . Trên tia đối của tia CA, lấy đoạn CD = CB. Tìm tập hợp các điểm D.
Chứng minh tam giác BCD đều \( \Rightarrow \widehat {ADB} = {60^0}\), từ đó suy ra quỹ tích điểm D.

Advertisements (Quảng cáo)
Ta có \(\widehat {ACB}\) là góc nội tiếp chắn cung 1200 \( \Rightarrow \widehat {ACB} = {120^0}\).
Mà \(\widehat {ACB} + \widehat {BCD} = {180^0}\)(kề bù) \( \Rightarrow \widehat {BCD} = {180^0} - {120^0} = {60^0}\).
Lại có \(CD = CB\,\,\left( {gt} \right) \Rightarrow \Delta BCD\) đều \( \Rightarrow \widehat {ADB} = {60^0}\).
Mà AB cố định \( \Rightarrow D\) di chuyển trên cung chứa góc 600 dựng trên đoạn thẳng AB.
Giới hạn : Khi \(C \equiv B \Rightarrow D \equiv B\)
Khi \(C \equiv A \Rightarrow D\) trùng với điểm chính giữa của cung lớn AB chứa góc 600 dựng trên đoạn AB.
