
Cho đường tròn (O) và hai dây cung AB, CD bằng nhau và cắt tại điểm M khác O nằm bên trong đường tròn (C nằm trên cung nhỏ AB và B nằm trên cung nhỏ CD).
a) Chứng minh cung AC=BD .
b) Chứng minh hai tam giác MAC và MDB bằng nhau.
c) Tứ giác ACBD là hình gì?
a) Cộng trừ cung.
b) Chứng minh hai tam giác MAC và MDB bằng nhau theo trường hợp g-c-g.
c) Chứng minh hai góc ở vị trí so le trong bằng nhau \( \Rightarrow AD//BC\).
Chứng minh hình thang ADBC có hai góc ở đáy bằng nhau.

Advertisements (Quảng cáo)
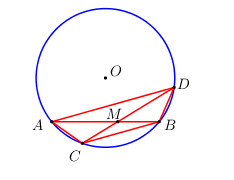
a) Ta có \(AB = CD \Rightarrow cung\,AB = cung\,CD\) (hai dây bằng nhau căng hai cung bằng nhau)
\( \Rightarrow cung\,AB - cung\,BC = cung\,CD - cung\,BC \Leftrightarrow cung\,AC = cung\,BD\).
b) Xét \(\Delta MAC\) và \(\Delta MDB\) có :
\(cung\,AC = cung\,BD \Rightarrow AC = BD\) (hai dây bằng nhau căng hai cung bằng nhau)
\(\widehat {MAC} = \widehat {MDB}\) (hai góc nội tiếp cùng chắn cung BC)
\(\widehat {MCA} = \widehat {MBD}\) (hai góc nội tiếp cùng chắn cung AD)
\( \Rightarrow \Delta MAC = \Delta MDB\,\,\left( {g.c.g} \right)\)
c) Ta có \(cung\,AC = cung\,BD \Rightarrow \widehat {ABC} = \widehat {BAD}\) (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
Mà hai góc này ở vị trí so le trong \( \Rightarrow AD//BC \Rightarrow ACBD\) là hình thang.
\(cung\,AB = cung\,CD \Rightarrow \widehat {ADB} = \widehat {CAD}\) (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
Do đó ACBD là hình thang cân.
