
Cho tam giác ABC nội tiếp đường tròn (O). Gọi D, E, F theo thứ tự là điểm chính giữa các cung AB, BC, CA. Chứng minh AE vuông góc với DF.
Góc có đỉnh ở bên trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn.

Advertisements (Quảng cáo)
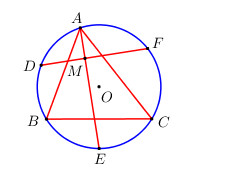
Gọi \(M = AE \cap DF\). Vì \(\widehat {DME}\) là góc có đỉnh ở bên trong đường tròn
\( \Rightarrow \widehat {DME} = \dfrac{{sdcung\,DE + sdcung\,AF}}{2} = \dfrac{{sdcung\,DB + sdcung\,BE + sdcung\,AF}}{2}\)
Ta có : \(sdcung\,DB = \dfrac{1}{2}sdcung\,AB;\,\,sdcung\,BE = \dfrac{1}{2}sdcung\,BC;\,\,sdcung\,AF = \dfrac{1}{2}sdcung\,AC\) (gt)
\( \Rightarrow \widehat {DME} = \dfrac{{\dfrac{1}{2}sdcung\,AB + \dfrac{1}{2}sdcung\,BC + \dfrac{1}{2}sdcung\,AC}}{2} = \dfrac{{\dfrac{1}{2}\left( {sdcung\,AB + sdcung\,BC + sdcung\,AC} \right)}}{2} = \dfrac{1}{4}{.360^0} = {90^0}\)
Vậy \(AE \bot DF\) (đpcm).
