
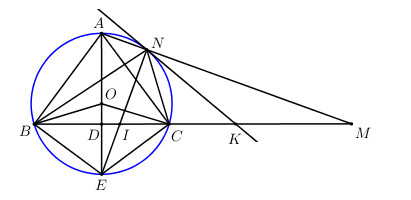
Cho tam giác ABC cân tại A và nội tiếp đường tròn O. Tia AO cắt BC và đường tròn O tại D và E.
a) Chứng minh \(AD \bot BC\) và EB = EC.
b) Trên cung nhỏ AC lấy điểm N sao cho AN < NC. Tia AN cắt tia BC tại M, tia NE cắt BC tại I. Chứng minh IB.IC = IE.IN và IB.MC = IC.MB.
c) Chứng minh \(\widehat {AMB} = \widehat {ACN}\) .
d) Tiếp tuyến tại N của đường tròn O cắt BM tại K. Chứng minh K là trung điểm của IM.
a) Chứng minh \(\Delta AOB = \Delta AOC\), chứng minh \(AO\) là phân giác của \(\widehat {BAC}\). Chúng minh \(\Delta ABE = \Delta ACE\).
b) +) Chứng minh .
+) Chứng minh NE và NM lần lượt là phân giác trong và ngoài của \(\widehat {BNC}\), sử dụng tính chất đường phân giác.
c) Chứng minh \(\widehat {AMB};\,\,\widehat {ACN}\) cùng bằng \(\widehat {AEN}\).
d) Chứng minh tam giác KIN và KMN cân tại K.

a) Xét \(\Delta AOB\) và \(\Delta AOC\) có:
\(\begin{array}{l}AB = AC\,\,\left( {gt} \right);\\OA\,\,chung;\\OB = OC = R;\end{array}\)
\( \Rightarrow \Delta AOB = \Delta AOC\,\,\left( {c.c.c} \right) \Rightarrow \widehat {OAB} = \widehat {OAC} \Rightarrow AO\) là tia phân giác của \(\widehat {BAC}\).
Mà tam giác ABC cân tại A \( \Rightarrow \) Phân giác AO đồng thời là đường cao \( \Rightarrow AO \bot BC\).
Mà \(D \in AO \Rightarrow AD \bot BC\).
Xét \(\Delta ABE\) và \(\Delta ACE\) có :
\(\begin{array}{l}AB = AC\,\,\left( {gt} \right);\\AE\,\,chung\\\widehat {BAE} = \widehat {CAE}\,\,\left( {cmt} \right);\end{array}\)
\( \Rightarrow \Delta ABE = \Delta ACE\,\,\left( {c.g.c} \right) \Rightarrow BE = CE\) (2 cạnh tương ứng).
b) +) Xét \(\Delta IBE\) và \(\Delta ICN\) có :
\(\widehat {BIE} = \widehat {NIC}\) (đối đỉnh) ;
Advertisements (Quảng cáo)
\(\widehat {IBE} = \widehat {INC}\) (hai góc nội tiếp cùng chắn cung IN) ;
\( \Rightarrow \Delta IBE \sim \Delta INC\,\,\left( {g.g} \right) \Rightarrow \dfrac{{IB}}{{IN}} = \dfrac{{IE}}{{IC}} \Rightarrow IB.IC = IE.IN\).
+) Ta có \(EB = EC\,\,\left( {cmt} \right) \Rightarrow cung\,EB = cung\,EC\) (hai dây bằng nhau căng 2 cung bằng nhau)
\( \Rightarrow \widehat {BNE} = \widehat {CNE}\) (trong 1 đường tròn, hai góc nội tiếp chắn 2 cung bằng nhau thì bằng nhau)
\( \Rightarrow NE\) là tia phân giác trong của \(\widehat {BNC}\).
Ta có: \(\widehat {ANE} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AN \bot NE\) hay \(NM \bot NE\).
Mà NE là tia phân giác trong của \(\widehat {BNC}\) (cmt) \( \Rightarrow NM\) là tia phân giác ngoài của \(\widehat {BNC}\).
Áp dụng tính chất tia phân giác ta có:
\(\dfrac{{NB}}{{NC}} = \dfrac{{IB}}{{IC}};\,\,\dfrac{{NB}}{{NC}} = \dfrac{{MB}}{{MC}} \Rightarrow \dfrac{{IB}}{{IC}} = \dfrac{{MB}}{{MC}} \Rightarrow IB.MC = IC.MB.\)
c) Xét \(\Delta ANE\) và \(\Delta ADM\) có:
\(\begin{array}{l}\widehat {ANE} = \widehat {ADM} = {90^0};\\\widehat {EMA}\,\,chung;\end{array}\)
\( \Rightarrow \Delta ANE \sim \Delta ADM\,\,\left( {g.g} \right) \Rightarrow \widehat {AEN} = \widehat {AMD}\) (hai góc tương ứng).
Mà \(\widehat {AEN} = \widehat {ACN}\) (hai góc nội tiếp cùng chắn cung AN)
\( \Rightarrow \widehat {ACN} = \widehat {AMD}\) (đpcm).
d) Xét \(\Delta EBI\) và \(\Delta ENB\) có:
\(\widehat {BEN}\,\,chung;\)
\(\widehat {EBI} = \widehat {ENB}\) (trong 1 đường tròn, hai góc nội tiếp chắn 2 cung bằng nhau thì bằng nhau)
\( \Rightarrow \Delta EBI \sim \Delta ENB\,\,\left( {g.g} \right) \Rightarrow \widehat {EIB} = \widehat {EBN}\).
Mà \(\widehat {EBN} = \widehat {ENK}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung EN).
\(\widehat {EIB} = \widehat {NIK}\) (đối đỉnh)
\( \Rightarrow \widehat {NIK} = \widehat {ENK} \Rightarrow \Delta KIN\) cân tại K \( \Rightarrow KN = KI\) (1).
Xét tam giác vuông MNI có: \(\widehat {NIK} + \widehat {KMN} = {90^0}\) (hai góc nhọn trong tam giác vuông phụ nhau)
\(\widehat {ENK} + \widehat {KNM} = \widehat {INM} = {90^0}\)
Mà \(\widehat {NIK} = \widehat {ENK}\,\,\left( {cmt} \right) \Rightarrow \widehat {KMN} = \widehat {KNM} \Rightarrow \Delta KMN\) cân tại K \( \Rightarrow KM = KN\) (2)
Từ (1) và (2) \( \Rightarrow KM = KI\). Vậy K là trung điểm của IM.
