
Cho hai đường tròn (O) và (O’) cắt nhau tại A và A’. Một cát tuyến qua A cắt (O) và (O’) lần lượt tại B và C. Vẽ hai đường thẳng song song lần lượt qua B, C và cắt (O) tại B’ và cắt (O’) tại C’. Chứng minh ba điểm A’, B’, C’ thẳng hàng.
+) Tứ giác ABB’A’ nội tiếp đường tròn (O), chứng minh \(\widehat {AA’B’} = {180^0} - \widehat {ABB’}\).
+) Tứ giác ACC’A’ nội tiếp đường tròn (O’), chứng minh \(\widehat {AA’C’} = {180^0} - \widehat {ACC’}\).
+) Chứng minh \(\widehat {B’A’C’} = \widehat {AA’B’} + \widehat {AA’C’} = {180^0}\).

Advertisements (Quảng cáo)
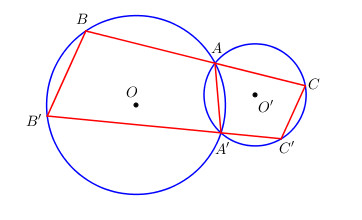
Tứ giác ABB’A’ nội tiếp đường tròn (O) \( \Rightarrow \widehat {AA’B’} + \widehat {ABB’} = {180^0}\) (tổng hai góc đối của tứ giác nội tiếp) \( \Rightarrow \widehat {AA’B’} = {180^0} - \widehat {ABB’}\).
Tứ giác ACC’A’ nội tiếp đường tròn (O’) \( \Rightarrow \widehat {AA’C’} + \widehat {ACC’} = {180^0}\) (tổng hai góc đối của tứ giác nội tiếp) \( \Rightarrow \widehat {AA’C’} = {180^0} - \widehat {ACC’}\).
\( \Rightarrow \widehat {AA’B’} + \widehat {AA’C’} = {180^0} - \widehat {ABB’} + {180^0} - \widehat {ACC’} = {360^0} - \left( {\widehat {ABB’} + \widehat {ACC’}} \right)\).
Vì BB’ // CC’ nên \(\widehat {ABB’} + \widehat {ACC’} = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat {AA’B’} + \widehat {AA’C’} = {360^0} - {180^0} = {180^0} \Rightarrow \widehat {B’A’C’} = {180^0}\).
Vậy A’, B’, C’ thẳng hàng.
