
Cho đường tròn (O), bán kính OA = 3 cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
Sử dụng định lí Pytago và quan hệ vuông góc giữa đường kính và dây cung.

Advertisements (Quảng cáo)
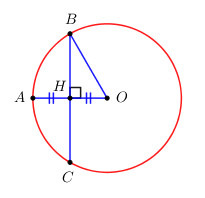
Gọi H là trung điểm của OA. Do H là trung điểm của OA \( \Rightarrow OH = \dfrac{1}{2}OA = \dfrac{3}{2}\,\,\left( {cm} \right)\)
Áp dụng định lí Pytago trong tam giác OBH có:
\(B{H^2} = O{B^2} - O{H^2} \)\(\,= {3^2} - {\left( {\dfrac{3}{2}} \right)^2} = \dfrac{{27}}{4}\)
\(\Leftrightarrow BH = \dfrac{{3\sqrt 3 }}{2}\,\,\left( {cm} \right)\).
Do \(OH \bot BC \Rightarrow H\) là trung điểm của BC (quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow BC = 2BH = 3\sqrt 3 \,\,\left( {cm} \right)\).
Baitapsgk.com
