
Cho đường tròn đường kính AB và dây EF không cắt đường kính. Gọi I và J lần lượt là chân các đường vuông góc kẻ từ A và B đến EF. Chứng minh IE = JF.
+) Kẻ \(OH//AI//BJ\), chứng minh \(HI = HJ\).
+) Chứng minh \(HE = HF\), từ đó suy ra \(IE = JF\).

Advertisements (Quảng cáo)
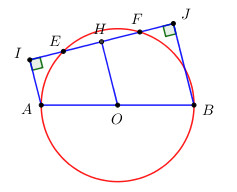
Ta có \(\left\{ \begin{array}{l}AI \bot EF\\BJ \bot EF\end{array} \right. \Rightarrow AI//BJ \Rightarrow AIJB\) là hình thang.
Kẻ \(OH//AI//BJ\), gọi \(O\) là trung điểm của AB, áp dụng tính chất đường trung bình của hình thang ta suy ra H là trung điểm của IJ \( \Rightarrow HI = HJ\) (1).
Ta có \(\left\{ \begin{array}{l}OH//AI\\AI \bot EF\end{array} \right. \Rightarrow OH \bot EF \Rightarrow H\) là trung điểm của \(EF\) (quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow HE = HF\) (2).
Từ (1) và (2) \( \Rightarrow HI - HE = HJ - HF\)
\(\Leftrightarrow IE = JF\).
Baitapsgk.com
