Advertisements (Quảng cáo)
Cho đường tròn tâm O, hai dây MN = PQ và hai đường thẳng MN, PQ cắt nhau tại A ở ngoài đường tròn (N nằm giữa M và A, Q nằm giữa P và A). Chứng minh AM = AP và AN = AQ.
+) Chứng minh AE = AF.
+) Cộng trừ đoạn thẳng, chú ý sử dụng định lí: Hai dây cách đều tâm thì bằng nhau.
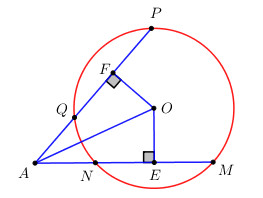
Kẻ \(OE \bot MN,\,\,OF \bot PQ\).
Do \(MN = PQ\,\,\left( {gt} \right) \) \(\Rightarrow OE = OF\) (trong một đường tròn, hai dây bằng nhau thì cách đều tâm).
Advertisements (Quảng cáo)
Xét tam giác vuông OAE và OAF có :
\(\begin{array}{l}OE = OF\,\,\left( {cmt} \right)\\OA\,\,chung\end{array}\)
\( \Rightarrow {\Delta _v}OAE = {\Delta _v}OAF\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow AE = AF\) (1) (2 cạnh tương ứng).
Ta có \(OE \bot MN;\,\,OF \bot PQ \Rightarrow \) E, F lần lượt là trung điểm của MN và PQ (quan hệ vuông góc giữa đường kính và dây cung) \( \Rightarrow EM = EN,\,\,FP = FQ\) (2)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}AE – EN = AF – FQ\\AE + EN = AF + FQ\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}AN = AQ\\AM = AP\end{array} \right.\).
Baitapsgk.com