
Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên đoạn AC, đường tròn đường kính CM cắt hai đường thẳng BM và BC lần lượt tại D và N, cắt đường thẳng AD tại S. Chứng minh:
a) Tứ giác ABCD nội tiếp.
b) Các đường thẳng AB, MN, CD đồng quy.
a) Chứng minh tứ giác ABCD có hai đỉnh A; D cùng nhìn AD dưới góc 900\( \Rightarrow A;D\) thuộc đường tròn đường kính BC.
b) Gọi E là giao điểm của AB và CD. Chứng minh ME và MN cùng vuông góc với BC suy ra E, M, N thẳng hàng.

Advertisements (Quảng cáo)
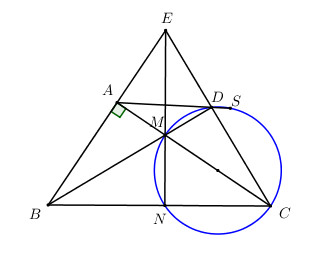
a) Ta có \(\widehat {BDC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính CM).
\( \Rightarrow \widehat {BDC} = \widehat {BAC} = {90^0} \Rightarrow \) Tứ giác ABCD có hai đỉnh A; D cùng nhìn AD dưới góc 900\( \Rightarrow A;D\) thuộc đường tròn đường kính BC.
\( \Rightarrow \) Tứ giác ABCD nội tiếp đường tròn đường kính BC.
b) Gọi E là giao điểm của AB và CD.
Xét \(\Delta EBC\) có \(BD \bot CE\,\,\left( {cmt} \right);\,\,AC \bot BE\,\,\left( {gt} \right);\,\,AC \cap BD = M \Rightarrow M\) là trực tâm của tam giác EBC \( \Rightarrow EM \bot BC\) (1)
Ta có \(\widehat {MNC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính MC) \( \Rightarrow MN \bot BC\) (2)
Từ (1) và (2) \( \Rightarrow \) Qua M kẻ được 2 đường thẳng MN và ME cùng vuông góc với BC \( \Rightarrow E;M;N\) thẳng hàng (tiên đề Ơ-clit).
Vậy AB, CD, MN đồng quy tại E.
