Advertisements (Quảng cáo)
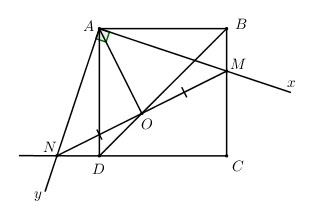
Cho hình vuông ABCD cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn BC tại M và tia Ay cắt đoạn CD kéo dài tại N.
a) Chứng minh hai tam giác ABM và AND bằng nhau.
b) Gọi O là trung điểm của MN. Chứng minh ABMO và ANDO là các tứ giác nội tiếp.
c) Chứng minh ba điểm B, D, O thẳng hàng.
a) Chứng minh \(\widehat {BAM} = \widehat {DAN}\), chứng minh \({\Delta _v}ABM\) và \({\Delta _v}ADN\) bằng nhau theo trường hợp cạnh góc vuông – góc nhọn.
b) Chứng minh tam giác AMN cân tại A \( \Rightarrow AO \bot MN\).
Chứng minh tứ giác ABMO có tổng hai góc đối bằng 1800.
Chứng minh tứ giác ANDO có hai đỉnh O; D cùng nhìn AN dưới góc 900.
c) Chứng minh hai góc ở vị trí đối đỉnh \(\widehat {BOM}\) và \(\widehat {DON}\) bằng nhau.
a) Ta có: \(\widehat {BAM} = \widehat {BAD} – \widehat {MAD} = {90^0} – \widehat {MAD}\).
\(\widehat {DAN} = \widehat {MAN} – \widehat {MAD} = {90^0} – \widehat {MAD}\)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {BAM} = \widehat {DAN}\)
Xét \({\Delta _v}ABM\) và \({\Delta _v}ADN\) có:
\(AB = AD\) (ABCD là hình vuông)
\(\widehat {BAM} = \widehat {DAN}\,\,\left( {cmt} \right)\);
\( \Rightarrow {\Delta _v}ABM = {\Delta _v}ADN\)(cạnh góc vuông – góc nhọn).
b) \({\Delta _v}ABM = {\Delta _v}ADN\,\,\left( {cmt} \right) \Rightarrow AM = AN\) (hai cạnh tương ứng) \( \Rightarrow \Delta AMN\) cân tại A.
\( \Rightarrow \) Trung tuyến AO đồng thời là đường cao \( \Rightarrow AO \bot MN \Rightarrow \widehat {AOM} = {90^0}\).
Xét tứ giác ABMO có: \(\widehat {AOM} + \widehat {ABM} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác ABMO là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
Xét tứ giác ANDO có: \(\widehat {AON} = \widehat {ADN} = {90^0} \Rightarrow \) Hai điểm O; D cùng nhìn AN dưới góc 900\( \Rightarrow A;D\) thuộc đường tròn đường kính AN \( \Rightarrow \) Tứ giác ANDO nội tiếp đường tròn đường kính AN.
c) Vì tứ giác ABMO nội tiếp (cmt) \( \Rightarrow \widehat {BOM} = \widehat {BAM}\) (hai góc nội tiếp cùng chắn cung BM).
Tứ giác ANDO nội tiếp (cmt) \( \Rightarrow \widehat {DON} = \widehat {DAN}\) (hai góc nội tiếp cùng chắn cung BN).
\({\Delta _v}ABM = {\Delta _v}ADN\,\,\left( {cmt} \right) \Rightarrow \widehat {BAM} = \widehat {DAN}\) (hai góc tương ứng)
\( \Rightarrow \widehat {BOM} = \widehat {DON}\). Mà 2 góc này ở vị trí hai góc đồng vị \( \Rightarrow B;D;O\) thẳng hàng.