Tính đô dài các đường phân giác trong và phân giác ngoài của một tam giác theo độ dài ba cạnh của tam giác đó.
Giải
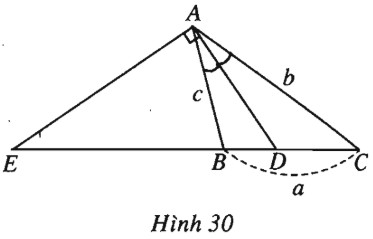
Xét tam giác \(ABC\) có \(AD, AE\) lần lượt là đường phân giác trong và ngoài (h.30). Theo bài 12a), ta có \(\overrightarrow {AD} = \dfrac{{b\overrightarrow {AB} + c\overrightarrow {AC} }}{{b + c}}.\) Bình phương vô hướng cả hai vế và sử dụng đẳng thức \(\overrightarrow {AB} .\overrightarrow {AC} = \dfrac{{{b^2} + {c^2} - {a^2}}}{2}\) (theo bài 14) để tính độ dài đoạn \(AD\). Vì \(AE\) là phân giác ngoài nên \(\overrightarrow {EB} = \dfrac{c}{b}\overrightarrow {EC} \) (lưu ý rằng phân giác ngoài của góc \(A\) chỉ cắt đường thẳng \(BC\) khi \(b \ne c\). Từ đó \(\overrightarrow {AE} = \dfrac{{b\overrightarrow {AB} - c\overrightarrow {AC} }}{{b - c}}.\) Ta suy ra
Advertisements (Quảng cáo)
\(\begin{array}{l}AD = \dfrac{2}{{b + c}}\sqrt {bcp(p - a)} ;\\AE = \dfrac{2}{{|b - c|}}\sqrt {bc(p - b)(p - c)} \end{array}\)
(\(p = \dfrac{{a + b + c}}{2}\) là nửa chu vi của tam giác).
