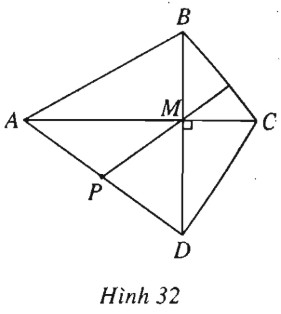
Tứ giác \(ABCD\) có hai đường chéo \(AC\) và \(BD\) vuông góc với nhau tại \(M\). Gọi \(P\) là trung điểm đoạn thẳng \(AD\). Chứng minh rằng : \(MP \bot BC\) khi và chỉ khi \(\overrightarrow {MA} .\overrightarrow {MC} = \overrightarrow {MB} .\overrightarrow {MD} .\)
Giải
(h.32).
\(\begin{array}{l}2\overrightarrow {MP} .\overrightarrow {BC} = (\overrightarrow {MA} + \overrightarrow {MD} ).(\overrightarrow {MC} - \overrightarrow {MB} )\\= \overrightarrow {MA} .\overrightarrow {MC} - \overrightarrow {MD} .\overrightarrow {MB} + \overrightarrow {MD} .\overrightarrow {MC} - \overrightarrow {MA} .\overrightarrow {MB} \\= \overrightarrow {MA} .\overrightarrow {MC} - \overrightarrow {MB} .\overrightarrow {MD} \end{array}\)
Advertisements (Quảng cáo)
( Do \(AC \bot BD\) nên \(\overrightarrow {MA} .\overrightarrow {MB} = \overrightarrow {MD} .\overrightarrow {MC} = 0\)).
Từ đó ta có
\(\begin{array}{l}MP \bot BC \Leftrightarrow \overrightarrow {MP} .\overrightarrow {BC} = 0\\\Leftrightarrow \overrightarrow {MA} .\overrightarrow {MC} = \overrightarrow {MB} .\overrightarrow {MD} .\end{array}\)
