Cho hình vuông \(ABCD\), điểm \(M\) nằm trên đoạn thẳng \(AC\) sao cho \(AM = \dfrac{{AC}}{4}\). Gọi \(N\) là trung điểm của đoạn thẳng \(DC\). Chứng minh rằng \(BMN\) là tam giác vuông cân.
Giải
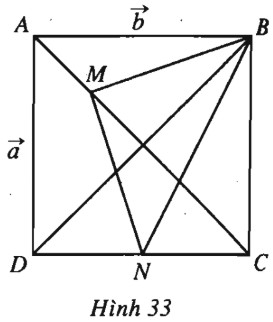
Đặt \(\overrightarrow {AD} = \overrightarrow a , \overrightarrow {AB} = \overrightarrow b .\) Khi đó, ta có
\(\overrightarrow {AM} = \dfrac{1}{4}\overrightarrow {AC} = \dfrac{1}{4}(\overrightarrow a + \overrightarrow b ),\)
\( \overrightarrow {AN} = \overrightarrow {AD} + \overrightarrow {DN} = \overrightarrow a + \dfrac{{\overrightarrow b }}{2}.\)
Advertisements (Quảng cáo)
Từ đó suy ra
\(\begin{array}{l}\overrightarrow {MB} = \overrightarrow {AB} - \overrightarrow {AM}\\ = \overrightarrow b - \dfrac{1}{4}(\overrightarrow a + \overrightarrow b )\\ = \dfrac{1}{4}( - \overrightarrow a + 3\overrightarrow b ).\\\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM}\\ = \overrightarrow a + \dfrac{{\overrightarrow b }}{2} - \dfrac{1}{4}(\overrightarrow a + \overrightarrow b ) \\= \dfrac{1}{4}(3\overrightarrow a + \overrightarrow b ).\end{array}\)
Ta có
\(\begin{array}{l}\overrightarrow {MB} .\overrightarrow {MN}\\ = \dfrac{1}{{16}}( - \overrightarrow a + 3\overrightarrow b )(3\overrightarrow a + \overrightarrow b )\\= \dfrac{1}{{16}}\left( { - 3\overrightarrow a + 3\overrightarrow b + 8\overrightarrow a .\overrightarrow b } \right) = 0.\\{\overrightarrow {MB} ^2} = \dfrac{1}{{16}}( - \overrightarrow a + 3\overrightarrow b ) \\= \dfrac{1}{{16}}({\overrightarrow a ^2} + 9{\overrightarrow b ^2} - 6\overrightarrow a .\overrightarrow b ) = \dfrac{5}{8}{\overrightarrow a ^2}.\\{\overrightarrow {MN} ^2} = \dfrac{1}{{16}}{\left( {3\overrightarrow a + \overrightarrow b } \right)^2}\\ = \dfrac{1}{{16}}\left( {9{{\overrightarrow a }^2} + {{\overrightarrow b }^2} + 6\overrightarrow a .\overrightarrow b } \right)\\ = \dfrac{5}{8}{\overrightarrow a ^2}.\end{array}\)
Vậy \(MB \bot MN\) và \(MB=MN\), tam giác \(BMN\) vuông cân tại đỉnh \(M.\)
