Cho \(AA’\) là một dây cung của đường tròn \((O)\) và \(M\) là một điểm nằm trên dây cung đó. Chứng minh rằng \(2\overrightarrow {MA} .\overrightarrow {MO} = MA(MA - MA’).\)
Giải
(h.34).
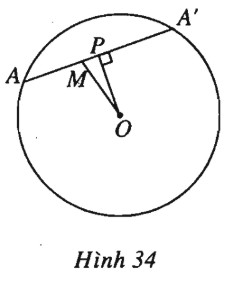
Gọi \(P\) là trung điểm của \(AA’\) thì \(OP \bot AA’\) nên theo công thức hình chiếu ta có
Advertisements (Quảng cáo)
\(2\overrightarrow {MA} .\overrightarrow {MO} = 2\overrightarrow {MA} .\overrightarrow {MP} \). Nhưng vì \(P\) là trung điểm của \(AA’\) nên \(2\overrightarrow {MP} = \overrightarrow {MA} + \overrightarrow {MA’} \).
Vậy:
\(\begin{array}{l}2\overrightarrow {MA} .\overrightarrow {MO} = \overrightarrow {MA} .(\overrightarrow {MA} + \overrightarrow {MA’} )\\ = M{A^2} + \overrightarrow {MA} .\overrightarrow {MA} ‘\\= M{A^2} - MA.MA’\\ = MA(MA - MA’).\end{array}\)
