Cho tam giác \(ABC\) không vuông.
a) Gọi \(AA’\) là đường cao của tam giác \(ABC\). Chứng minh \(\left( {{\mathop{\rm tanB}\nolimits} } \right)\overrightarrow {A’B} + \left( {\tan C} \right)\overrightarrow {A’C} = \overrightarrow 0 \)
b) Gọi \(H\) là trực tâm tam giác \(ABC.\) Chứng minh
\((\tan A)\overrightarrow {HA} + (\tan B)\overrightarrow {HB} \)\( + (\tan C)\overrightarrow {HC} = \overrightarrow 0 \).

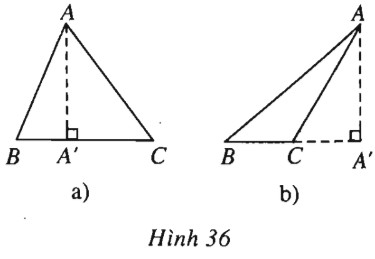
a) Xét trường hợp điểm \(A’\) nằm trên cạnh \(BC\), tức là các góc \(B\) và \(C\) đều nhọn (h.36a).
Khi đó
\(AA’ = A’B.\tan B = A’C.\tan C.\)
Vì \(\tan B > 0, \tan C > 0\) và hai vec tơ \(\overrightarrow {A’B} ; \overrightarrow {A’C} \) ngược hướng nên ta suy ra
\((\tan B)\overrightarrow {A’B} + (\tan C)\overrightarrow {A’C} = \overrightarrow 0 (*)\)
Nếu điểm \(A’\) nằm ngoài cạnh \(BC\), chẳng hạn điểm \(C\) nằm giữa hai điểm \(B\) và \(A’\) (h.36b), thì khi đó góc \(B\) nhọn và góc \(C\) tù, tức là \(\tan B > 0\) và \(\tan C < 0\).
Ta có
Advertisements (Quảng cáo)
\(AA’ = A’B\tan B\)
\(= A’C\tan ({180^0} - C)\)
\(= - A’C\tan C.\)
Trong trường hợp này hai vec tơ \(\overrightarrow {A’B} ; \overrightarrow {A’C} \) cùng hướng nên ta có : \((\tan B)\overrightarrow {A’B} + (\tan C)\overrightarrow {A’C} = \overrightarrow 0 \).
b) Nếu \(H\) là trực tâm tam giác \(ABC\) thì ta có các số \(\alpha , \beta , \gamma \) không đồng thời bằng 0 sao cho :\(\alpha \overrightarrow {HA} + \beta \overrightarrow {HB} + \gamma \overrightarrow {HC} = \overrightarrow 0 \) (theo bài 14 chương I). Vì \(AH \bot BC\) nên nhân hai vế của đẳng thức trên với \(\overrightarrow {BC} \) ta được \(\beta \overrightarrow {HB} .\overrightarrow {BC} + \gamma \overrightarrow {HC} .\overrightarrow {BC} = \overrightarrow 0 \) và do đó ta có ( theo công thức hình chiếu):
\(\begin{array}{l}\beta \overrightarrow {A’B} .\overrightarrow {BC} + \gamma \overrightarrow {A’C} .\overrightarrow {BC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {BC} (\beta \overrightarrow {A’B} + \gamma \overrightarrow {A’C} ) = \overrightarrow 0 \\ \Leftrightarrow \beta \overrightarrow {A’B} + \gamma \overrightarrow {A’C} = \overrightarrow 0 \end{array}\)
(vì vec tơ\(\beta \overrightarrow {A’B} + \gamma \overrightarrow {A’C} \) cùng phương với \(\overrightarrow {BC} \)).
So sánh đẳng thức này với (*) ta suy ra \(\dfrac{\beta }{{\tan B}} = \dfrac{\gamma }{{\tan C}}\). Bằng cách tương tự ta đi đến:
\(\dfrac{\alpha }{{\tan A}} = \dfrac{\beta }{{\tan B}} = \dfrac{\gamma }{{\tan C}}\).
Bởi vậy đẳng thức \(\alpha \overrightarrow {HA} + \beta \overrightarrow {HB} + \gamma \overrightarrow {HC} = \overrightarrow 0 \) trở thành
\(\tan A.\overrightarrow {HA} + \tan B.\overrightarrow {HB} \)\( + \tan C.\overrightarrow {HC} = \overrightarrow 0 .\)
