Cho điểm \(O\) bất kì nằm trong tam giác \(A_1A_2A_3\). Gọi \(B_1, B_2, B_3\) lần lượt là hình chiếu của \(O\) trên \(A_1A_2, A_2A_3, A_3A_1\). Đặt
\(\begin{array}{l}\overrightarrow {{a_1}} = {A_1}{A_2}\dfrac{{\overrightarrow {O{B_1}} }}{{O{B_1}}} ,\\\overrightarrow {{a_2}} = {A_2}{A_3}\dfrac{{\overrightarrow {O{B_2}} }}{{O{B_2}}} ,\\\overrightarrow {{a_3}} = {A_3}{A_1}\dfrac{{\overrightarrow {O{B_3}} }}{{O{B_3}}} .\end{array}\)
Chứng minh rằng \(\overrightarrow {{a_1}} + \overrightarrow {{a_2}} + \overrightarrow {{a_3}} = \overrightarrow 0 \).
Chú ý: kết quả trên đúng với đa giác \(A_1A_2…A_n\) bất kì (định lí Con Nhím). Trên hình 23, \(|\overrightarrow {{a_k}} | = {A_k}{A_{k + 1}}\) ( xem \({A_{n + 1}} \equiv {A_1}\)), \(\overrightarrow {{a_1}} + \overrightarrow {{a_2}} + ... + \overrightarrow {{a_n}} = \overrightarrow 0 \) (các vec tơ \(\overrightarrow {{a_k}} \) được gọi là các “ lông nhím”).
Giải
(h.37).
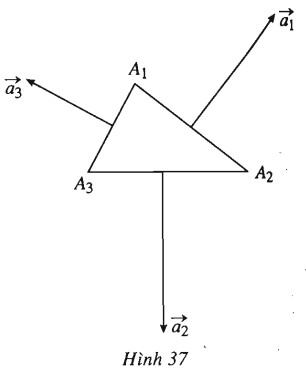
Ta có
Advertisements (Quảng cáo)
\(\begin{array}{l}\left( {\overrightarrow {{a_1}} + \overrightarrow {{a_2}} + \overrightarrow {{a_3}} } \right).\overrightarrow {{A_1}{A_2}} \\ = \left( {\overrightarrow {{a_2}} + \overrightarrow {{a_3}} } \right).\overrightarrow {{A_1}{A_2}} \\= \left( {\overrightarrow {{a_2}} + \overrightarrow {{a_3}} } \right)\left( {\overrightarrow {{A_1}{A_3}} - \overrightarrow {{A_2}{A_3}} } \right)\\= \overrightarrow {{a_2}} .\overrightarrow {{A_1}{A_3}} - \overrightarrow {{a_3}} .\overrightarrow {{A_2}{A_3}} \\= |\overrightarrow {{a_2}} |{A_1}{A_3}.\cos \left( {\overrightarrow {{a_2}} ,\overrightarrow {{A_1}{A_3}} } \right) \\- |\overrightarrow {{a_3}} |.{A_2}{A_3}.\cos \left( {\overrightarrow {{a_3}} ,\overrightarrow {{A_2}{A_3}} } \right).\\\end{array}\)
Theo giả thiết \(|\overrightarrow {{a_2}} | = {A_2}{A_3} , |\overrightarrow {{a_3}} | = {A_1}{A_3}\).
Ngoài ra dễ thấy \(\cos \left( {\overrightarrow {{a_2}} ,\overrightarrow {{A_1}{A_3}} } \right) = \cos \left( {\overrightarrow {{a_3}} ,\overrightarrow {{A_2}{A_3}} } \right).\)
Suy ra \(\left( {\overrightarrow {{a_1}} + \overrightarrow {{a_2}} + \overrightarrow {{a_3}} } \right).\overrightarrow {{A_1}{A_2}} = 0\). Do đó, vec tơ \(\overrightarrow {{a_1}} + \overrightarrow {{a_2}} + \overrightarrow {{a_3}} \) vuông góc với đường thẳng \(A_1A_2\).
Chứng minh hoàn toàn tương tự, ta có vec tơ \(\overrightarrow {{a_1}} + \overrightarrow {{a_2}} + \overrightarrow {{a_3}} \) vuông góc với đường thẳng \(A_2A_3\).
Vậy \(\overrightarrow {{a_1}} + \overrightarrow {{a_2}} + \overrightarrow {{a_3}} = 0\).
