Bài 33 trang 43 Sách bài tập Toán Nâng cao Hình 10: (h.39)....

Cho điểm $P$ cố định nằm trong đường tròn $(O ; R)$ và hai điểm $A, B$ chạy trên đường tròn đó sao cho góc $APB$ luôn bằng $90^0$. Gọi $M$ là trung điểm của dây $AB$ và $H$ là hình chiếu của $P$ xuống $AB$. Chứng minh rằng $M ,H$  luôn cùng thuộc một đường tròn cố định.

(h.39).

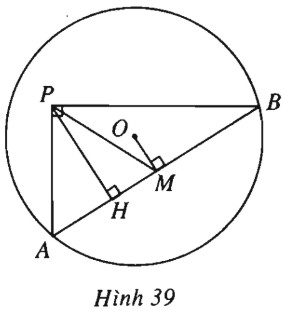
Ta có ${\wp _{H/(O)}} = \overrightarrow {HA} .\overrightarrow {HB}  =  - H{P^2}$ và ${\wp _{H/(O)}} = H{O^2} - {R^2}$, suy ra .. hay $H{O^2} + H{P^2} = {R^2}$.        (*)

Tương tự ${\wp _{M/(O)}} = \overrightarrow {MA} .\overrightarrow {MB}  =  - M{B^2}$ và ${\wp _{M/(O)}} = M{O^2} - {R^2}$.

Mặt khác tam giác vuông $APB$ có trung tuyến $MP = \dfrac{1}{2}AB = MB$.

Từ đó suy ra $M{O^2} - {R^2} =  - M{P^2}$ hay $M{O^2} + M{P^2} = {R^2}$.          (**)

Từ (*) và (**) ta có $H, M$ cùng thuộc đường tròn có tâm là trung điểm của $OP$ và bán kính bằng $\dfrac{1}{2}\sqrt {2{R^2} - O{P^2}}$.