Bài 34 trang 43 SBT Hình học 10 Nâng cao. Do \((c+CK)+(b+BK)\)\(=a+b+c=2p\) nên \(c+CK=p\) hay \(CK=p-c=BH.\). Bài 2. Tích vô hướng của hai vec tơ
Cho tam giác \(ABC\) ngoại tiếp đường tròn \((I)\) và \((J)\) là đường tròn bàng tiếp góc \(A\)(*) của tam giác. Chứng minh rằng trục đẳng phương của hai đường tròn đó đi qua trung điểm của cạnh \(BC.\)
Giải
Đặt tên các tiếp điểm của hai đường tròn như hình 40.
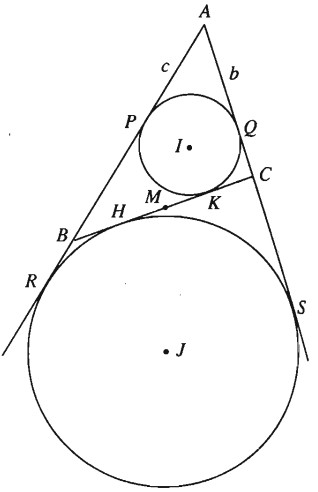
Ta có \(AR=AS\) và
\(AR+AS=(AB+BR)+(AC+CS)\)
\(=(AB+BH)+(AC+CH)\)
Advertisements (Quảng cáo)
\(=AB+BC+AC=2p.\)
Vậy \(AR=AS=p,\) suy ra \(c+BH=p\) hay \(BH=p-c.\)
Ta cũng có \(AP=AQ, BP=BK, CK=CQ\) nên \(c+CK=b+BK.\)
Do \((c+CK)+(b+BK)\)\(=a+b+c=2p\) nên \(c+CK=p\) hay \(CK=p-c=BH.\)
Gọi \(M\) là trung điểm của \(BC,\) từ \(BH=CK\) suy ra \(MH=MK\) hay \({P_{M/(I)}} = M{K^2} = M{H^2} = {P_{M/(J)}}.\)
Vậy \(M\) thuộc trục đẳng phương của hai đường tròn \((I)\) và \((J)\).