Cho đường tròn đường kính \(AB\) và đường thẳng \(\Delta \) vuông góc với \(AB\) ở \(H\) (\(H\) không trùng với \(A\) và \(B\)). Một đường thẳng quay quanh \(H\) cắt đường tròn ở \(M, N\) và các đường thẳng \(AM, AN\) lần lượt cắt \(\Delta \) ở \(M’, N’.\)
a) Chứng minh rằng bốn điểm \(M, N, M’, N’\) cùng thuộc một đường tròn \((C)\) nào đó.
b) Chứng minh rằng các đường tròn \((C)\) luôn đi qua hai điểm cố định.
Giải
(h.42).
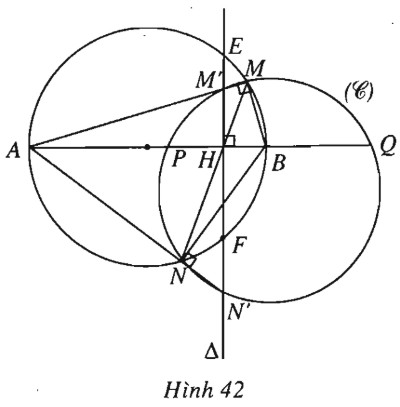
a) Tứ giác \(HBMM’\) nội tiếp được do \(\widehat {M’HB} = \widehat {M’MB} = {90^0}\), suy ra \(\overrightarrow {AH} .\overrightarrow {AB} = \overrightarrow {AM} .\overrightarrow {AM’} .\)
Tứ giác \(HBN’N\) cũng nội tiếp được do \(\widehat {N’HB} = \widehat {N’NB} = {90^0}\), suy ra \(\overrightarrow {AH} .\overrightarrow {AB} = \overrightarrow {AN} .\overrightarrow {AN’} .\)
Advertisements (Quảng cáo)
Từ đó ta có \(\overrightarrow {AM} .\overrightarrow {AM’} = \overrightarrow {AN} .\overrightarrow {AN’} \)
Suy ra \(M, N, M’, N’\) cùng thuộc một đường tròn, ta kí hiệu đường tròn đó là \((C).\)
b) Gọi \(P, Q\) là các giao điểm của \((C)\) với đường thẳng \(AB\) và \(E, F\) là các giao điểm của \(\Delta \) với đường tròn đường kính \(AB.\)
Khi đó
\(\overrightarrow {HE} .\overrightarrow {HF} = \overrightarrow {HM} .\overrightarrow {HN} = \overrightarrow {HP} .\overrightarrow {HQ} \) nên \(E, P, F, Q\) cùng thuộc đường tròn \((S)\). Đường tròn này tiếp xúc với \(AE, AF\) lần lượt tại \(E, F\) và do \(AE, AF\) đối xứng qua \(AB\) nên \((S)\) cố định, suy ra \(P, Q\) là hai điểm cố định.
Vậy \(P, Q\) thuộc đường tròn \((S)\) tiếp xúc với \(AE, AF\) ở \(E, F.\)
Do \((S)\) là đường tròn cố định nên \(P, Q\) là hai điểm cố định của \((C).\)
