Bài 38 trang 44 SBT Hình học 10 Nâng cao. Cho đường tròn đường kính \(AB, H\) là điểm nằm giữa \(AB\) và đường thẳng \(\Delta \) vuông góc với \(AB\) tại \(H.\) Gọi \(E, F\). Bài 2. Tích vô hướng của hai vec tơ
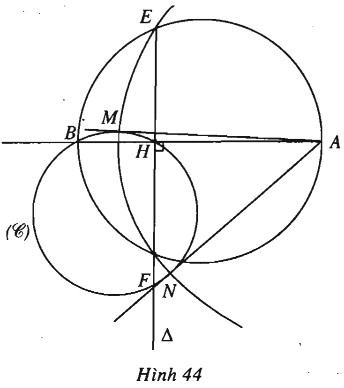
Cho đường tròn đường kính \(AB, H\) là điểm nằm giữa \(AB\) và đường thẳng \(\Delta \) vuông góc với \(AB\) tại \(H.\) Gọi \(E, F\) là giao điểm của đường tròn và \(\Delta \). Vẽ đường tròn tâm \(A,\) bán kính \(AE\) và đường tròn \((C)\) bất kì qua \(H, B\). Giả sử hai đường tròn đó cắt nhau ở \(M\) và \(N\), chứng minh rằng \(AM\) và \(AN\) là hai tiếp tuyến của \((C)\).
Giải
(h.44).
Advertisements (Quảng cáo)
Ta có \(AM=AN=AE\) (do \(M, N, E\) cùng thuộc đường tròn tâm \(A\)). Trong tam giác vuông \(AEB,\) \(EH \bot AB\) nên \(A{E^2} = AH.AB = \overrightarrow {AH} .\overrightarrow {AB} \).
Từ đó suy ra \(A{M^2} = A{N^2} = \overrightarrow {AH} .\overrightarrow {AB} \).
Vậy \(AM, AN\) là tiếp tuyến của \((C)\) (xem bài 30 chương II).