Cho đường tròn \((O ; R)\) và điểm \(A\) không thuộc đường tròn đó. Đường thẳng \(\Delta \) quay quanh \(A\) cắt \((O ; R)\) ở \(M\) và \(N\). Xác định vị trí của \(\Delta \) để một trong ba điểm \(A, M, N\) cách đều hai điểm kia.
Giải
(h.43).
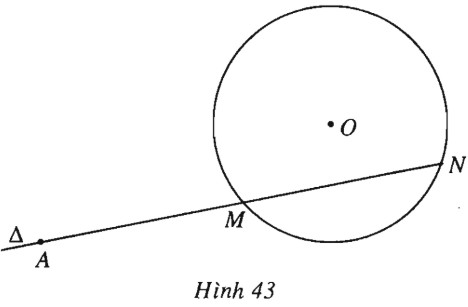
Nếu \(A\) ở ngoài đường tròn thi điều kiện \(AM=MN\) tương đương với \(AN=2AM.\)
Ta lại có \(AM.AN=d^2-R^2 (d=OA).\)
Advertisements (Quảng cáo)
Từ đó dẫn đến \(2AM^2=d^2-R^2\) hay \(AM = \dfrac{{\sqrt {2({d^2} - {R^2})} }}{2}\).
Điểm \(M\) (nếu có) là một điểm chung của đường tròn \((O ; R)\) và đường tròn tâm \(A\), bán kính bằng \(\dfrac{{\sqrt {2({d^2} - {R^2})} }}{2}\).
Nếu A nằm trong đường tròn thì đường thẳng \(\Delta \) cần tìm là:
- Đường thẳng vuông góc với \(OA\) ở \(A\) khi \(A\) không trùng với \(O.\)
- Đường kính bất kì của đường tròn khi \(A\) trùng với \(O.\)
