Advertisements (Quảng cáo)
Cho hai điểm \(P, Q\) nằm ngoài đường tròn \((I)\) cố định với \(IP \ne IQ\).
a) Vẽ đường tròn \((C)\) bất kì đi qua \(P, Q\). Chứng minh rằng trục đẳng phương của \((C)\) và \((I)\) đi qua một điểm cố định.
b) Hãy nêu cách vẽ đường tròn đi qua \(P, Q\) và tiếp xúc với đường tròn \((I)\).
Giải
a) (h.45).
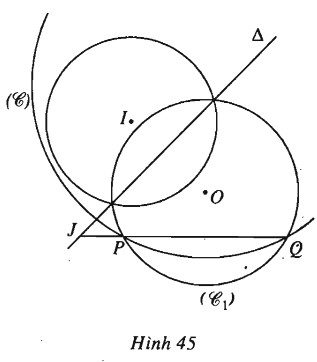
Gọi \((C_1)\) là đường tròn cố định có tâm \(O\) và đi qua \(P, Q.\) Do \(I\) không thuộc đường trung trực của \(PQ\) nên trục đẳng phương \(\Delta \) của \((C_1)\) và \((I)\) không song song với \(PQ\), chúng phải cắt nhau ở \(J\).
Bây giờ giả sử \((C)\) là đường tròn bất kì đi qua \(P\) và \(Q\), ta có \(J\) thuộc trục đẳng phương \(PQ\) của \((C)\) và \((C_1)\) nên \({P_{J/(C)}} = {P_{J/({C_1})}}\).
Advertisements (Quảng cáo)
Lại có \(J\) thuộc trục đẳng phương của \((C_1)\) và \((I)\) nên \({P_{J/({C_1})}} = {P_{J/(I)}}\).
Từ đó ta có \({P_{J/(C)}} = {P_{J/(I)}}\), hay \(J\) thuộc trục đẳng phương của \((C)\) và \((I).\)
b) (h.46).
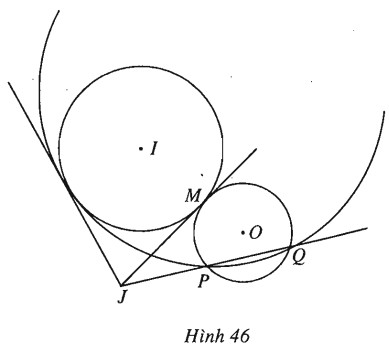
Kẻ tiếp tuyến \(JM\) với \((I)\) (\(M\) là tiếp điểm), ta có \(J{M^2} = {P_{J/(I)}}.\)
Do \({P_{J/(I)}} = \overrightarrow {JP} .\overrightarrow {JQ} \) nên đường tròn \((MPQ)\) tiếp xúc với \(JM\) ở \(M\) và cũng tiếp xúc với \((I)\) ở \(M\). Từ đó suy ra cách dựng. Bài toán có hai nghiệm.