Advertisements (Quảng cáo)
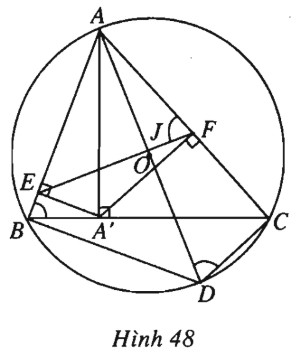
Cho tam giác \(ABC\) nội tiếp trong đường tròn \((O ; R)\), có đường cao \(AA’\). Gọi \(E, F\) tương ứng là hình chiếu của \(A’\) trên \(AB, AC\) và \(J\) là giao điểm của \(EF\) với đường kính \(AD.\)
a) Chứng minh rằng \(AA’\) là tiếp tuyến của đường tròn \((A’JD).\)
b) Tìm điều kiện của \(AA’\) để ba điểm \(E, F, O\) thẳng hàng.
Giải
(h.48).
Advertisements (Quảng cáo)
a) Trong hai tam giác vuông \(AA’B\) và \(AA’C\) ta có \(\overrightarrow {AE} .\overrightarrow {AB} = AA{‘^2}\) và \(\overrightarrow {AF} .\overrightarrow {AC} = AA{‘^2}\) nên \(\overrightarrow {AE} .\overrightarrow {AB} = \overrightarrow {AF} .\overrightarrow {AC} \), suy ra tứ giác \(BEFC\) nội tiếp được, do đó ta có\(\widehat {AFE} = \widehat {ABC}\).
Mặt khác \(\widehat {ABC} = \widehat {ADC}\) ( góc nội tiếp cùng chắn cung \(AC\)) nên tứ giác \(DCFJ\) nội tiếp được, suy ra \(\overrightarrow {AJ} .\overrightarrow {AD} = \overrightarrow {AF} .\overrightarrow {AC} \). Vậy \(\overrightarrow {AJ} .\overrightarrow {AD} = AA{‘^2}\) do đó \(AA’\) là tiếp tuyến của đường tròn \((A’JD).\)
b) Ba điểm \(E, F, O\) thẳng hàng khi \(O\) trùng với \(J\) hay \(AJ=R.\)
Do \(\overrightarrow {AJ} .\overrightarrow {AD} = AA{‘^2}\) nên \(AJ=R\) nếu \(AA’^2=2R^2\) hay \(AA’ = R\sqrt 2 \).