Cho điểm \(M\) cố định trên đường tròn \((O ; R)\) và hai điểm \(N, P\) chạy trên đường tròn đó sao cho \(\widehat {NMP} = {30^0}\).
a) Tìm quỹ tích trung điểm \(I\) của \(NP.\)
b) Xác định vị trí của \(N, P\) để diện tích tam giác \(MNP\) đạt giá trị lớn nhất.
Giải
(h.59).
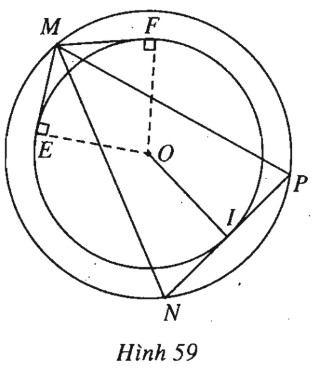
a) Ta có \(NP = 2R\sin {30^0} = R,\)
\( O{I^2} = O{N^2} - N{I^2} \)
Advertisements (Quảng cáo)
\(= {R^2} - \dfrac{{{R^2}}}{4} = \dfrac{{3{R^2}}}{4}\).
Suy ra \(OI = \dfrac{{R\sqrt 3 }}{2}\) không đổi, do đó \(I\) thuộc đường tròn tâm \(O\) bán kính bằng \(\dfrac{{R\sqrt 3 }}{2}\).
Đảo lại, với mỗi điểm \(I\) trên đường tròn đó ta kẻ dây cung \(NP\) của \((O)\) vuông góc với \(OI\) thì \(NP=2NI=R.\)
Ta có \(\sin \widehat {NMP} = \dfrac{R}{{2R}} = \dfrac{1}{2}\). Góc \(NMP\) có thể bằng \(30^0\) hoặc bằng \(150^0\). Dễ thấy \(\widehat {NMP} = {30^0}\) khi và chỉ khi \(O, M\) ở về một phía của \(NP\) hay \(I\) nằm trên cung lớn \(\stackrel\frown {EF}\) của đường tròn \(\left( {O ; \dfrac{{R\sqrt 3 }}{2}} \right)\) (\(E, F\) là hai tiếp điểm của hai tiếp tuyến kẻ từ M tới đường tròn \(\left( {O ; \dfrac{{R\sqrt 3 }}{2}} \right)\) ).
Vậy quỹ tích của \(I\) là cung lớn \(\stackrel\frown {EF}\).
b) Diện tích tam giác MNP là \(S = \dfrac{1}{2}MN.MP.{\mathop{\rm s}\nolimits} {\rm{i}}{{\rm{n}}^0} = \dfrac{1}{4}MN.MP\). Theo bất đẳng thức Cô-si, \(MN.MP \le \dfrac{{M{N^2} + M{P^2}}}{2}\), mà \(M{N^2} + M{P^2} = 2M{I^2} + \dfrac{{{R^2}}}{2}\) nên \(S \le \dfrac{1}{4}\left( {M{I^2} + \dfrac{{{R^2}}}{4}} \right)\). (*)
Ta có \(MI\) lớn nhất khi \(M, O, I\) thẳng hàng và \(O\) nằm giữa \(M, I\). Khi đó ta cũng có \(MN=MP\) nên (*) xảy ra dấu “=”. Vậy \(S\) lớn nhất khi và chỉ khi \(MI\) lớn nhất hay \(M ,O, I\) thẳng hàng và \(O\) nằm giữa \(M, I.\)
