Kẻ các đường cao \(AA’, BB’, CC’\) của tam giác nhọn \(ABC.\)
a) Chứng minh rằng \(B’C’ = 2R\sin A\cos A\).
b) Lấy \(A_1, A_2\) lần lượt là điểm đối xứng với \(A’\) qua \(AB, AC\). Chứng minh rằng chu vi tam giác \(A’B’C’\) bằng độ dài đoạn thẳng \(A_1A_2\).
c) Chứng minh hệ thức:
\(\sin A\cos A + \sin B\cos B + \sin C\cos C \)
\(= 2\sin A\sin B\sin C\).
Giải
(h.60).
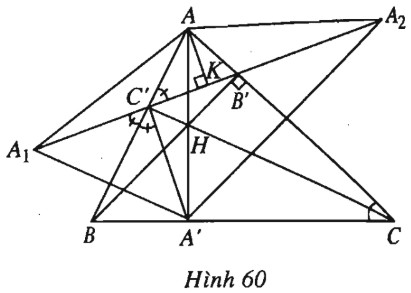
a) Ta có
\(AB’=AB\cos A=2R \sin C \cos A.\)
Trong tam giác \(AB’C’\) có \(\dfrac{{B’C’}}{{\sin A}} = \dfrac{{AB’}}{{\sin C’}}\).
Nhưng \(\widehat {AC’B’} = \widehat C\) (do \(BC’B’C\) là tứ giác nội tiếp), suy ra \(\dfrac{{B’C’}}{{\sin A}} = \dfrac{{AB’}}{{\sin C}}\).
Từ đó suy ra
\(B’C’ = \dfrac{{AB’\sin A}}{{\sin C’}}\)
\(= \dfrac{{2R\sin C\cos A\sin A}}{{\sin C}}\)
\(= 2R\sin A\cos A\).
Advertisements (Quảng cáo)
b) Ta có \(\widehat {{A_1}C’B} = \widehat {BC’A’}\) (do \(A_1, A’\) đối xứng với nhau qua \(AB\)).
\(\widehat {BC’A’} = \widehat {AC’B’}\) (do \(AC’A’C\) và \(BC’B’C\) cùng là tứ giác nội tiếp).
Suy ra \(\widehat {{A_1}C’B} = \widehat {B’C’A}\). Vậy \(A_1, C’, B’\) thẳng hàng và \(A_1C’=A’C’.\)
Tương tự cũng có \(C’, B’, A_2\) thẳng hàng và \(B’A_2=B’A’.\)
Do đó, chu vi tam giác \(A’B’C’\) bằng
\(A’C’+C’B’+B’A’\)
\(=A_1C’+C’B’+B’A_2=A_1A_2\).
c) Do \(A_1\) và \(A’\) đối xứng nhau qua \(AB\) nên \(A{A_1} = AA’ , \widehat {{A_1}AB} = \widehat {BAA’}\); \(A_2\) và \(A’\) đối xứng nhau qua \(AC\) nên \(A{A_2} = AA’ , \widehat {A’AC} = \widehat {CA{A_2}}\). Do đó tam giác \(AA_1A_2\)là tam giác cân có góc ở đỉnh \(\widehat {{A_1}A{A_2}} = 2\widehat A\). Kẻ \(AK\) vuông góc với \(A_1A_2\), ta có
\(A_1A_2=2A_1K\)
\(=2AA_1 \sin A=2AA’\sin A\)
\(=2AB\sin B\sin A\)
\(=4R\sin C\sin B\sin A.\)
Mặt khác theo câu a), ta có
\(B’C’+B’A’+A’C’\)
\(=2R \sin A \cos A+2R \sin C \cos C\)\(+2R \sin B \cos B.\)
Từ đó suy ra hệ thức cần chứng minh.
