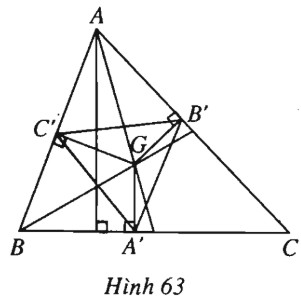
Cho tam giác \(ABC\) có trọng tâm \(G\). Gọi \(A’, B’, C’\) lần lượt là hình chiếu của \(G\) trên các cạnh \(BC, CA, AB\) của tam giác. Hãy tính diện tích của tam giác \(A’B’C’\) biết rằng tam giác \(ABC\) có diện tích bằng \(S\) và khoảng cách từ \(G\) đến tâm đường tròn ngoại tiếp tam giác đó bằng \(d\), bán kính đường tròn ngoại tiếp bằng \(R.\)
Giải
(h.63).
\({S_{A’B’C’}} = {S_{GA’B’}} + {S_{GB’C’}} + {S_{GC’A’}} ;\)
\( {S_{GA’B’}} = \dfrac{1}{2}.GA’.GB’.\sin ({180^0} - \widehat C)\)
\(= \dfrac{1}{{18}}{h_a}{h_b}\sin C\).
Advertisements (Quảng cáo)
Trong tam giác ABC, \({h_a} = \dfrac{{2S}}{a} , {h_b} = \dfrac{{2S}}{b} , \sin C = \dfrac{c}{{2R}}\)
Từ đó ta có \({S_{GA’B’}} = \dfrac{{{S^2}.c}}{{9ab.R}} = \dfrac{{{S^2}.{c^2}}}{{9abc.R}}\).
Tương tự, \({S_{GB’C’}} = \dfrac{{{S^2}{a^2}}}{{9abc.R}} ; {S_{GC’A’}} = \dfrac{{{S^2}{b^2}}}{{9abc.R}}\).
Suy ra \({S_{A’B’C’}} = \dfrac{{{S^2}}}{{9abc.R}}({a^2} + {b^2} + {c^2}).\)
Ta lại có \(S = \dfrac{{abc}}{{4R}}\) và \({a^2} + {b^2} + {c^2} = 9({R^2} - {d^2})\) ( theo bài 64) nên \({S_{A’B’C’}} = \dfrac{{{R^2} - {d^2}}}{{4{R^2}}}.S\).
