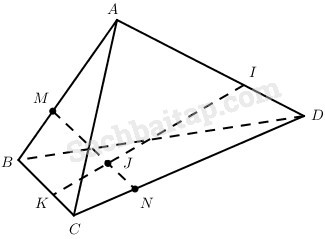
Cho tứ diện ABCD, M và N là các điểm lần lượt thuộc AB và CD sao cho \(\overrightarrow {MA} = - 2\overrightarrow {MB} ,\,\overrightarrow {N{\rm{D}}} = - 2\overrightarrow {NC} \). Các điểm I, J, K lần lượt thuộc AD, MN, BC sao cho \(\overrightarrow {IA} = k\overrightarrow {I{\rm{D}}} ,\,\overrightarrow {JM} = k\overrightarrow {JN} ,\,\overrightarrow {KB} = k\overrightarrow {KC} \). Chứng minh rằng các điểm I, J, K thẳng hàng.

Cách 1.
Ta có:
\(\eqalign{ & \overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AM} + \overrightarrow {MJ} \,\,\,\,\,\,\,\,\,\left( 1 \right) \cr & \overrightarrow {IJ} = \overrightarrow {ID} + \overrightarrow {DN} + \overrightarrow {NJ} \,\,\,\,\,\,\,\,\,\,\,\left( 2 \right) \cr} \)
Từ (2) ta có:
\(\eqalign{ & k\overrightarrow {IJ} = k\overrightarrow {ID} + k\overrightarrow {DN} + k\overrightarrow {NJ} \cr & hay\,\,\,k\overrightarrow {IJ}= \overrightarrow{IA} + k\overrightarrow {DN} + \overrightarrow {MJ} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right) \cr} \)
Từ (1), (3) ta có:
\(\eqalign{ & \left( {1 - k} \right)\overrightarrow {IJ} = \overrightarrow {AM} - k\overrightarrow {DN} \cr & hay\,\,\overrightarrow {IJ} = {1 \over {1 - k}}\overrightarrow {AM} - {k \over {1 - k}}\overrightarrow {DN} \cr} \)
Chứng minh tương tự như trên, ta có:
\(\overrightarrow {JK} = {1 \over {1 - k}}\overrightarrow {MB} - {k \over {1 - k}}\overrightarrow {NC} \)
Mặt khác \(\overrightarrow {MA} = - 2\overrightarrow {MB} ,\,\,\,\overrightarrow {N{\rm{D}}} = - 2\overrightarrow {NC} \)
Advertisements (Quảng cáo)
nên \(\overrightarrow {IJ} = {2 \over {1 - k}}\overrightarrow {MB} - {{2k} \over {1 - k}}\overrightarrow {NC} \).
Từ đó, ta có \(\overrightarrow {IJ} = 2\overrightarrow {IK} \)
Vậy ba điểm I, J, K thẳng hàng.
Cách 2.
Vì \(\overrightarrow {MA} = - 2\overrightarrow {MB} \)
nên với điểm O bất kì thì \(\overrightarrow {OM} = {{\overrightarrow {OA} + 2\overrightarrow {OB} } \over 3}\).
Tương tự
\(\eqalign{ & \overrightarrow {ON} = {{\overrightarrow {O{\rm{D}}} + 2\overrightarrow {OC} } \over 3};\,\,\,\overrightarrow {OI} = {{\overrightarrow {OA} - k\overrightarrow {O{\rm{D}}} } \over {1 - k}}; \cr & \overrightarrow {OK} = {{\overrightarrow {OB} - k\overrightarrow {OC} } \over {1 - k}};\,\,\overrightarrow {OJ} = {{\overrightarrow {OM} - k\overrightarrow {ON} } \over {1 - k}}. \cr} \)
Từ đó, ta có:
\(\eqalign{ & \overrightarrow {OJ} = {1 \over {1 - k}}.{1 \over 3}\left( {\overrightarrow {OA} + 2\overrightarrow {OB} - k\overrightarrow {OD} - 2k\overrightarrow {OC} } \right) \cr & = {1 \over {1 - k}}.{1 \over 3}\left[ {\left( {1 - k} \right)\overrightarrow {OI} + 2\left( {1 - k} \right)\overrightarrow {OK} } \right] \cr & = {1 \over 3}(\overrightarrow {OI} + 2\overrightarrow {OK} ) = {1 \over 3}\overrightarrow {OI} + {2 \over 3}\overrightarrow {OK} . \cr} \)
Mặt khác \({1 \over 3} + {2 \over 3} = 1\).
Vậy 3 điểm I, J, K thẳng hàng.
