Cho hình lăng trụ ABC. A’B’C’. Gọi I và J lần lượt là trung điểm của BB’ và A’C’. Điểm K thuộc B’C’ sao cho \(\overrightarrow {KC’} = - 2\overrightarrow {KB’} \) . Chứng minh rằng bốn điểm A, I, J, K cùng thuộc một mặt phẳng.

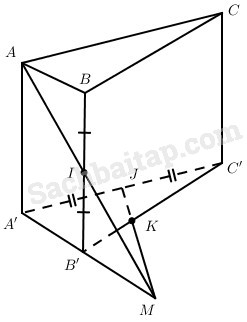
Đặt \(\overrightarrow {AA’} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c .\)
Ta có:
Advertisements (Quảng cáo)
\(\eqalign{ & \overrightarrow {AI} = {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {AB’} } \right) \cr & = {1 \over 2}\left( {\overrightarrow b + \overrightarrow a + \overrightarrow b } \right) \cr & = {1 \over 2}\left( {\overrightarrow a + 2\overrightarrow b } \right);\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \cr & \overrightarrow {AJ} = {1 \over 2}\left( {\overrightarrow {AA’} + \overrightarrow {AC’} } \right) \cr & = {1 \over 2}\left( {\overrightarrow a + \overrightarrow a + \overrightarrow c } \right) \cr & = {1 \over 2}\left( {2\overrightarrow a + \overrightarrow c } \right).\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right) \cr & \overrightarrow {AK} = {{\overrightarrow {AC’} + 2\overrightarrow {AB’} } \over 3} \cr & = {{\overrightarrow a + \overrightarrow c + 2\left( {\overrightarrow a + \overrightarrow b } \right)} \over 3} \cr & = {{3\overrightarrow a + 2\overrightarrow b + \overrightarrow c } \over 3}.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right) \cr} \)
Từ (1), (2), (3) ta có \(\overrightarrow {AK} = {2 \over 3}\left( {\overrightarrow {AI} + \overrightarrow {AJ} } \right)\)
Vậy \(\overrightarrow {AI} ,\overrightarrow {AJ} ,\overrightarrow {AK} \) đồng phẳng, tức là các điểm A, I, J, K cùng thuộc một mặt phẳng.
Chú ý: Có thể chứng minh các điểm A, I, J, K thuộc một mặt phẳng bằng cách chứng minh AI và JK cắt nhau tại điểm M.
