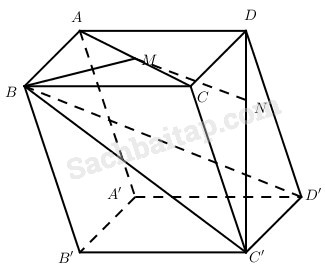
Cho hình hộp ABCD.A’B’C’D’; các điểm M, N lần lượt thuộc các đường thẳng CA và DC’ sao cho \(\overrightarrow {MC} - m\overrightarrow {MA} ,\,\overrightarrow {N{\rm{D}}} = m\overrightarrow {NC’} \). Xác định m để các đường thẳng MN và BD’ song song với nhau. Khi ấy, tính MN biết \(\widehat {ABC} = \widehat {ABB’} = \widehat {CBB’} = {60^0}\) và BA = a, BB’ = b, BC = c.

Xác định m:
Đặt \(\overrightarrow {BA} = \overrightarrow a ,\,\overrightarrow {BB} = \overrightarrow b ,\,\overrightarrow {BC} = \overrightarrow c \) thì \(\overrightarrow {B{\rm{D}}’} = \overrightarrow a + \overrightarrow b + \overrightarrow {c.} \)
Do \(\overrightarrow {MC} = m\overrightarrow {MA} \) nên \(\overrightarrow {BM} = {{\overrightarrow {BC} - m\overrightarrow {BA} } \over {1 - m}} = {{\overrightarrow c - m\overrightarrow a } \over {1 - m}}\)
Tương tự, ta có:
\(\eqalign{ & \overrightarrow {BN} = {{\overrightarrow {B{\rm{D}}} - m\overrightarrow {BC’} } \over {1 - m}} = {{\overrightarrow a + \overrightarrow c - m\left( {\overrightarrow b + \overrightarrow c } \right)} \over {1 - m}} \cr & = {1 \over {1 - m}}\overrightarrow a - {m \over {1 - m}}\overrightarrow b + \overrightarrow c . \cr} \)
Từ đó
\(\eqalign{ & \overrightarrow {MN} = \overrightarrow {BN} - \overrightarrow {BM} \cr & = {{1 + m} \over {1 - m}}\overrightarrow a - {m \over {1 - m}}\overrightarrow b - {m \over {1 - m}}\overrightarrow c . \cr} \)
Do AC, BD’ chéo nhau và DC’, BD’ chéo nhau nên
\(\eqalign{ & MN//B{\rm{D}}’ \Leftrightarrow \overrightarrow {MN} = k\overrightarrow {B{\rm{D}}’} \cr & \Leftrightarrow \overrightarrow {MN} = k\overrightarrow a + k\overrightarrow b + k\overrightarrow c \cr} \)
Advertisements (Quảng cáo)
Mặt khác \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng nên điều ấy xảy ra khi và chỉ khi:
\(\eqalign{ & \left\{ \matrix{ {{1 + m} \over {1 - m}} = k \hfill \cr - {m \over {1 - m}} = k \hfill \cr - {m \over {1 - m}} = k \hfill \cr} \right. \cr & \Rightarrow 1 + m = - m \Leftrightarrow m = - {1 \over 2} \cr} \)
Từ đó, ta có \(k = {1 \over 3}\)
Vậy \(m = - {1 \over 2}\) thì MN // BD’.
Tính MN:
Khi ấy \(\overrightarrow {MN} = {1 \over 3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\)
do đó
\({\overrightarrow {MN} ^2} \)
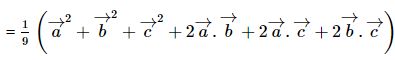
hay \(M{N^2} = {1 \over 9}\left( {{a^2} + {b^2} + {c^2} + ab + ac + bc} \right)\)
tức là \(MN = {1 \over 3}\sqrt {{a^2} + {b^2} + {c^2} + ab + bc + ca} \)
