21. Trang 8 Sách bài tập Hình Học 11 nâng cao.
Cho hai đoạn thẳng bằng nhau AB = A’B’. Chứng minh rằng có thể tìm được một phép đối xứng trục hoặc hợp thành của hai phép đối xứng trục để biến A thành A’, biến B thành B’.

Advertisements (Quảng cáo)
Nếu A và A’ trùng nhau, B và B’ trùng nhau thì phép cần tìm là phép đối xứng trục có trục AB.
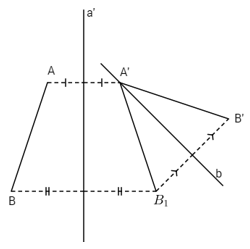
Nếu A không trùng A’ thì ta lấy a là trung trực của AA’. Khi đó phép đối xứng trục \({Đ_a}\) biến A thành A’. Kí hiệu \({B_1}\) là ảnh của B qua phép \({Đ_a}\). Nếu \({B_1}\) trùng B’ thì \({Đ_a}\) là phép đối xứng trục cần tìm. Nếu \({B_1}\) khác B’ thì \(A'{B_1} = AB\) nên \(A'{B_1} = A’B’\). Từ đó, suy ra đường trung trực b của đoạn thẳng \({B_1}B’\) đi qua điểm A’ và do đó phép đối xứng trục \({Đ_b}\) biến A’ thành A’ và biến \({B_1}\) thành B’.
Vậy hợp thành của hai phép đối xứng trục \({Đ_a}\) và \({Đ_b}\) là phép dời hình biến A thành A’ và biến B thành B’.
