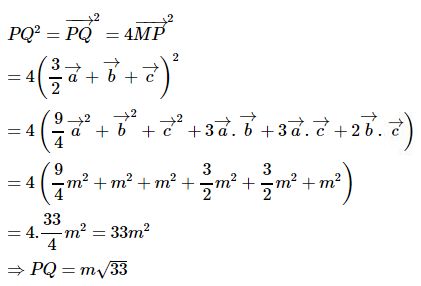Cho hình hộp ABCD.A’B’C’D’ có các cạnh bằng m, các góc tại A bằng 600 \(\left( {\widehat {BA{\rm{D}}} = \widehat {A’AB} = \widehat {A’A{\rm{D}}} = {{60}^0}} \right)\) . Gọi P và Q là các điểm xác định bởi \(\overrightarrow {AP} = \overrightarrow {D’A} ,\overrightarrow {C’Q} = \overrightarrow {DC’} \). Chứng minh rằng đường thẳng PQ đi qua trung điểm của cạnh BB’. Tính độ dài đoạn thẳng PQ.

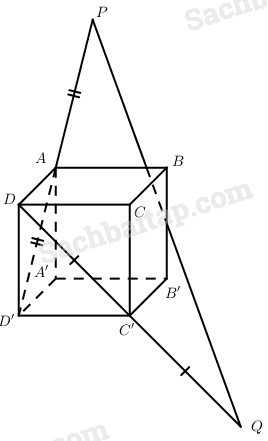
Đặt \(\overrightarrow {AA’} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c \) .
Ta có: \(\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow c = \overrightarrow c .\overrightarrow a = {1 \over 2}{m^2}\)
và \({\overrightarrow a ^2} = {\overrightarrow b ^2} = {\overrightarrow c ^2} = {m^2}\) .
Gọi M là trung điểm của BB’ thì
\(\overrightarrow {MP} = \overrightarrow {MB} + \overrightarrow {BA} + \overrightarrow {AP} \).
Do \(\overrightarrow {AP} = \overrightarrow {D’A} = - \overrightarrow a - \overrightarrow c \).
Advertisements (Quảng cáo)
nên
\(\eqalign{ & \overrightarrow {MP} = - {{\overrightarrow a } \over 2} - \overrightarrow b - \overrightarrow a - \overrightarrow c \cr & = - {3 \over 2}\overrightarrow a - \overrightarrow b - \overrightarrow c \cr} \)
Mặt khác
\(\eqalign{
& \overrightarrow {MQ} = \overrightarrow {MB’} + \overrightarrow {B’C’} + \overrightarrow {C’Q} \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {MB’} + \overrightarrow {B’C’} + \overrightarrow {DC’} \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = {3 \over 2}\overrightarrow a + \overrightarrow b + \overrightarrow c \cr} \)
Như vậy \(\overrightarrow {MP} = - \overrightarrow {MQ} \) , tức là ba điểm P, M, Q thẳng hàng hay đường thẳng PQ đi qua trung điểm của cạnh BB’.
Ta có: