Cho hình lập phương ABCD.A’B’C’D’. Gọi M và N lần lượt là các điểm thuộc AD’ và DB sao cho \(\overrightarrow {MA} = k\overrightarrow {M{\rm{D}}’} ,\overrightarrow {N{\rm{D}}} = k\overrightarrow {NB} \left( {k \ne 0,k \ne 1} \right)\).
a) Chứng minh rằng MN luôn song song với mp (A’BC).
b) Khi đường thẳng MN song song với đường thẳng A’C, chứng tỏ rằng MN vuông góc với AD’ và DB

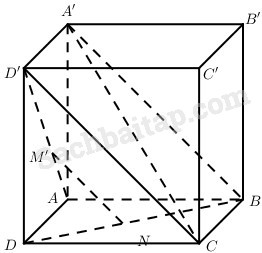
a) Đặt \(\overrightarrow {AA’} = \overrightarrow a ,\,\overrightarrow {AB} = \overrightarrow b ,\,\overrightarrow {AD} = \overrightarrow c \).
Khi đó, ta có:
\(\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow c = \overrightarrow c .\overrightarrow a = 0\).
và \({\overrightarrow a ^2} = {\overrightarrow b ^2} = {\overrightarrow c ^2}\).
Vì \(\overrightarrow {MA} = k\overrightarrow {M{\rm{D}}’} \) nên \(\overrightarrow {MA} = k\left( {\overrightarrow {MA} + \overrightarrow {A{\rm{D}}’} } \right)\).
Vậy \(\overrightarrow {AM} = {k \over {k - 1}}\left( {\overrightarrow a + \overrightarrow c } \right).\)
Tương tự như trên, ta có:
\(\overrightarrow {AN} = {{\overrightarrow {A{\rm{D}}} - k\overrightarrow {AB} } \over {1 - k}} = - {k \over {1 - k}}\overrightarrow b + {1 \over {1 - k}}\overrightarrow c \).
Từ đó: \(\eqalign{ & \overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} \cr & = {{1 + k} \over {1 - k}}\overrightarrow c + {k \over {1 - k}}\left( {\overrightarrow a - \overrightarrow b } \right) \cr} \)
hay \(\overrightarrow {MN} = {{1 + k} \over {1 - k}}\overrightarrow {BC} + {k \over {1 - k}}\overrightarrow {BA’} \).
Advertisements (Quảng cáo)
Như vậy ba vectơ \(\overrightarrow {MN} ,\overrightarrow {BC} ,\overrightarrow {BA’} \) đồng phẳng.
Mặt khác AD’, DB cắt mp(A’BCD’); các điểm M, N lần lượt thuộc AD’, DB với k ≠ 0, k ≠ 1 nên MN không thuộc mp(A’BC). Vậy MN song song với mp(A’BC).
b) Ta có \(\overrightarrow {A’C} = - \overrightarrow a + \overrightarrow b + \overrightarrow c \); A’C, AD’ chéo nhau; A’C, BD chéo nhau mà \(M \in A{\rm{D}}’,N \in DB\). Do đó, đường thẳng MN song song với đường thẳng A’C khi và chỉ khi \(\overrightarrow {MN} = m\overrightarrow {A’C} \) , tức là
\({k \over {1 - k}}\overrightarrow a - {k \over {1 - k}}\overrightarrow b + {{1 + k} \over {1 - k}}\overrightarrow c = - m\overrightarrow a + m\overrightarrow b + m\overrightarrow c \)
Do \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) là ba vectơ không đồng phẳng nên đẳng thức trên xảy ra khi bà chỉ khi
\(\left\{ \matrix{ {k \over {1 - k}} = - m \hfill \cr - {k \over {1 - k}} = m \hfill \cr {{1 + k} \over {1 - k}} = m \hfill \cr} \right.\)
Suy ra \( - k = 1 + k \Leftrightarrow k = - {1 \over 2}\)
Vậy khi \(k = - {1 \over 2}\) thì MN song song với A’C.
Khi đó \(\overrightarrow {MN} = - {1 \over 3}\left( {\overrightarrow a - \overrightarrow b - \overrightarrow c } \right)\)
Mặt khác \(\overrightarrow {A{\rm{D}}’} = \overrightarrow a + \overrightarrow c ,\overrightarrow {DB} = \overrightarrow b - \overrightarrow c \)
Vậy
\(\eqalign{ & \overrightarrow {MN} .\overrightarrow {A{\rm{D}}’} = - {1 \over 3}\left( {{{\overrightarrow a }^2} - {{\overrightarrow c }^2}} \right) = 0 \cr & \overrightarrow {MN} .\overrightarrow {DB} = - {1 \over 3}\left( { - {{\overrightarrow b }^2} + {{\overrightarrow c }^2}} \right) = 0 \cr} \)
Điều này khẳng định MN vuông góc với AD’ và DB.
