Câu 6 trang 114 Sách bài tập Hình học 11 Nâng cao. Đặt →AA′=→a,→AB=→b,→AD=→c. Bài 1. Vectơ trong không gian. Sự đồng phẳng của các vectơ
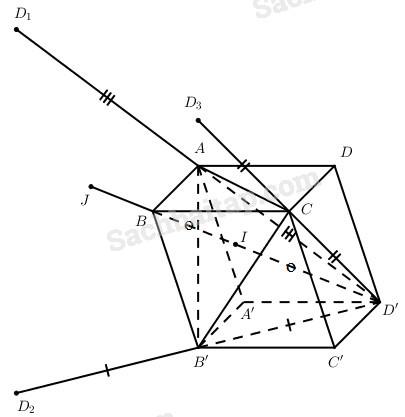
Cho hình hộp ABCD.A’B’C’D’. Gọi D1,D2,D3 lần lượt là điểm đối xứng của điểm D’ qua A, B’, C. Chứng tỏ rằng B là trọng tâm của tứ diện D1D2D3D′.
Cách 1.
Đặt →AA′=→a,→AB=→b,→AD=→c
Từ giả thiết, ta có
→BD′+→BD1=2→BA=−2→b
mà →BD′=→a−→b+→c
Vậy →BD1=−→a−→b−→c.
Advertisements (Quảng cáo)
Lập luận tương tự như trên, ta có →BD2=→a+→b−→c và →BD3=−→a+→b+→c
Vậy →BD1+→BD2+→BD3+→BD′=→0
Điều này chứng tỏ B là trọng tâm của tứ diện D1D2D3D′ .
Cách 2.
Gọi I là giao điểm của BD’ và mp(AB’C) thì D’I = 2IB.
Gọi J là giao điểm của BD’ với mp (D1D2D3), do D1, D2, D3 là các điểm đối xứng của D’ lần lượt qua A, B’, C nên IJ = ID’ hay D′B=34D′J.
Mặt khác I là trọng tâm tam giác AB’C nên J là trọng tâm tam giác D1D2D3. Từ đó B là trọng tâm của tứ diện D1D2D3D′.