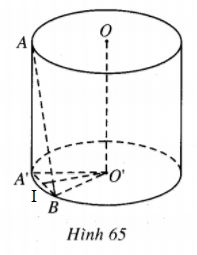
Cho hình trụ có bán kính đáy bằng R, chiều cao OO’ bằng h, A và B là hai điểm thay đổi trên hai đường tròn đáy sao cho AB = a không đổi \(\left( {h < a < \sqrt {{h^2} + 4{R^2}} } \right)\).
1) Chứng minh góc giữa hai đường thẳng AB và OO’ không đổi.
2) Chứng minh khoảng cách giữa hai đường thẳng AB và OO’ không đổi.

Advertisements (Quảng cáo)
1) Gọi AA’ là một đường sinh của hình trụ thì AA’=h và \({\rm{AA’//}}OO’\), khi ấy \(\alpha = \widehat {BAA’}\) là góc giữa AB và OO’ và \(\cos \alpha = {{AA’} \over {AB}} = {h \over a}.\)
Điều này khẳng định góc giữa AB và OO’ không đổi.
2) Gọi I là trung điểm của A’B thì có \(O’I \bot mp(AA’B),\) mặt khác \(OO’//mp(AA’B),\) vậy O’I là khoảng cách giữa AB và OO’.
Vì O’I là trung tuyến của tam giác A’O’B có ba cạnh là \(A’B = \sqrt {{a^2} - {h^2}} ,O’A’ = O’B’ = R\) nên O’I có độ dài không đổi. Dễ thấy \(O’I = \sqrt {{R^2} - {{{a^2} - {h^2}} \over 4}} .\)
