Cho hình trụ có bán kính đáy bằng R, thiết diện qua trục của hình trụ là hình vuông.
1) Tính diện tích và thể tích hình cầu ngoại tiếp hình trụ.
2) Một mp(P) song song với trục hình trụ, cắt đáy hình trụ theo một dây cung có độ dài bằng bán kính đáy hình trụ. Tính diện tích các thiết diện của hình trụ và hình cầu ngoại tiếp hình trụ khi cắt bởi mặt phẳng (P).

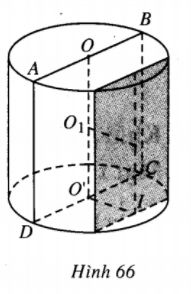
1) Giả sử thiết diện qua trục OO’ của hình trụ là hình vuông ABCD. Khi đó AB = AD = 2R. Gọi O1 là trung điểm của OO’ thì mặt cầu tâm O1, bán kính O1B là mặt cầu ngoại tiếp hình trụ.
Dễ thấy \({O_1}B = R\sqrt 2 \).
Advertisements (Quảng cáo)
Vậy diện tích mặt cầu là \(4\pi {\left( {R\sqrt 2 } \right)^2} = 8\pi {R^2}\) và thể tích khối cầu là \({4 \over 3}\pi {\left( {R\sqrt 2 } \right)^2} = {8 \over 3}\pi {R^3}\sqrt 2 .\)
2) Mặt phẳng (P) song song với OO’ nên cắt hình trụ theo thiết diện là hình chữ nhật có một cạnh bằng AD, cạnh còn lại theo giả thiết bằng R.
Vậy diện tích thiết diện của hình trụ cắt bởi (P) là \(R.2R = 2{R^2}.\)
Vì \((P)//OO’\) nên khoảng cách từ tâm O1 của mặt cầu ngoại tiếp hình trụ đến (P) bằng khoảng cách từ O’ đến (P) và bằng O’I (I là trung điểm của dây cung nói trong giả thiết ).
Ta có \(O'{I^2} = {R^2} - {\left( {{R \over 2}} \right)^2} = {{3{R^2}} \over 4}.\) Tức là \(O’I = {{R\sqrt 3 } \over 2}.\) Vì mp(P) cắt mặt cầu trên theo đường tròn nên bán kính r của đường tròn được tính theo công thức :
\({r^2} = {O_1}{B^2} - O'{I^2} = 2{R^2} - {{3{R^2}} \over 4} = {{5{R^2}} \over 4}.\)
Vậy diện tích thiết diện của mặt cầu ngoại tiếp hình trụ đã cho khi cắt bởi mp(P) là \(S = {{5\pi {R^2}} \over 4}.\)
