Cho hìnhchữ nhật ABCD với AB = a, BC = 2a và đường thẳng \(\Delta \) nằm trong mặt phẳng (ABCD), \(\Delta \) song song với AD và cách AD một khoảng bằng x, \(\Delta \) không có điểm chung với hình chữ nhật ABCD.
1) Tính thể tích của hình tròn xoay tạo nên khi quay hình chữ nhật ABCD quanh \(\Delta \).
2) Xác định x để thể tích nói trên gấp ba lần thể tích hình cầu có bán kính bằng cạnh AB.

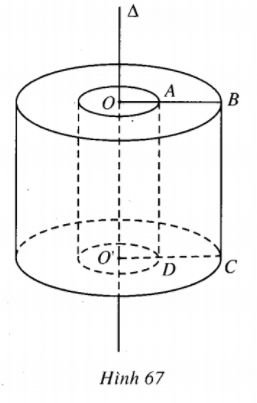
1) Kí hiệu O, O’ lần lượt là giao điểm của các đường thẳng AB, CD với \(\Delta \). Gọi V là thể tích cần tìm, V2 là thể tích hình trụ tạo nên khi quay hình chữ nhật OBCO’ quanh \(\Delta \) ( với OA < OB) hoặc hình tạo nên khi quay hình chữ nhật OADO’ quanh \(\Delta \) (với OA > OB); V1 là thể tích hình trụ tạo nên khi quay hình chữ nhật OADO’ quanh \(\Delta \) ( với OA < OB) hoặc hình trụ tạo nên khi quay hình chữ nhật OBCO’ quanh \(\Delta \) ( với OA > OB). Khi đó V = V2 - V1.
Từ đó, với OA < OB thì
\(V = \pi O{B^2}.BC - \pi O{A^2}.AD\)
\(= 2a\pi \left[ {{{(x + a)}^2} - {x^2}} \right] \)
Advertisements (Quảng cáo)
\(= 2{a^2}\pi (2x + a)\)
và với OA > OB thì
\(V = \pi O{A^2}.AD - \pi O{B^2}.BC \)
\(= 2a\pi \left[ {{x^2}-{{(x - a)}^2} } \right] \)
\(= 2{a^2}\pi (2x - a)\)
2) Thể tích khối cầu bán kính bằng AB là \({4 \over 3}\pi {a^3}\).Theo giả thiết ta có
\(4\pi {a^3} = 2\pi {a^2}(2x + a)\) (với OA < OB)
Hoặc \(4\pi {a^3} = 2\pi {a^2}(2x - a)\) ( với OA > OB).
Từ đó \(x = {a \over 2}\) ( với OA < OB) hoặc \(x = {{3a} \over 2}\) ( với OA > OB).
