Cho hình lập phương ABCD.A’B’C’D’ cạnh a.
a) Chứng minh \({A’C} \bot (AB’D’).\)
b) Gọi M là trung điểm của AD, N là trung điểm của BB’. Chứng minh \(A’C \bot MN.\)
c) Tính cô sin của góc giữa hai vec tơ \(\overrightarrow {MN} \) và \(\overrightarrow {AC’} \).
d) Tính \({V_{A’CMN}}\)

Thiết lập hệ trục tọa độ như hình vẽ (h.97).Ta có
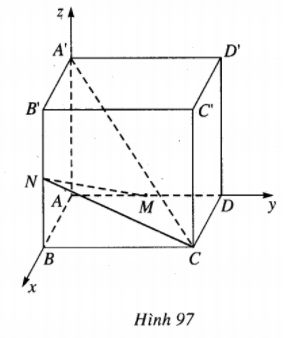
A(0;0;0); A’(0;0;a); C’(a;a;a); D(0;a;0)
B(a;0;0); D’(0;a;a); B’(a;0;a), C(a;a;0).
Advertisements (Quảng cáo)
a) Ta có :
\(\eqalign{ & \overrightarrow {A’C} = (a;a; - a), \cr & \overrightarrow {AB’} = (a;0;a),\overrightarrow {AD’} = (0;a;a) \cr & \Rightarrow \overrightarrow {A’C} .\overrightarrow {AB’} = 0,\overrightarrow {A’C} .\overrightarrow {AD’} = 0 \cr & \Rightarrow \overrightarrow {A’C} \bot \overrightarrow {{\rm{AB’}}} ,\overrightarrow {A’C} \bot \overrightarrow {AD’} \cr & \Rightarrow A’C \bot mp(AB’D’). \cr} \)
b) Ta lại có :
\(\eqalign{ & N(a;0;{a \over 2}),M\left( {0;{a \over 2};0} \right) \Rightarrow \overrightarrow {MN} = \left( {a; - {a \over 2};{a \over 2}} \right) \cr & \Rightarrow \overrightarrow {MN} .\overrightarrow {A’C} = {a^2} - {{{a^2}} \over 2} - {{{a^2}} \over 2} = 0 \Rightarrow MN \bot A’C. \cr} \)
c) \(\overrightarrow {AC’} = (a;a;a)\) nên
\(\cos \left( {\overrightarrow {MN} ,\overrightarrow {AC’} } \right) = {{\overrightarrow {MN} .\overrightarrow {AC’} } \over {\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {AC’} } \right|}} = {{{a^2} - {{{a^2}} \over 2} + {{{a^2}} \over 2}} \over {\sqrt {{{3{a^2}} \over 2}} .\sqrt {3{a^2}} }} = {{\sqrt 2 } \over 3}\)
d) \(\eqalign{ & {V_{A’CMN}} = {1 \over 6}\left| {\left[ {\overrightarrow {A’N} .\overrightarrow {A’M} } \right].\overrightarrow {A’C} } \right|. \cr & \cr} \)
Ta có :
\(\eqalign{ & \overrightarrow {A’N} = (a;0; - {a \over 2}),\overrightarrow {A’M} = \left( {0;{a \over 2}; - a} \right). \cr & \left[ {\overrightarrow {A’N} ,\overrightarrow {A’M} } \right] = \left( {\left| \matrix{ 0 \hfill \cr {a \over 2} \hfill \cr} \right.\left. \matrix{ - {a \over 2} \hfill \cr - a \hfill \cr} \right|;\left| \matrix{ - {a \over 2} \hfill \cr a \hfill \cr} \right.\left. \matrix{ a \hfill \cr \hfill \cr 0 \hfill \cr} \right|;\left| \matrix{ a \hfill \cr \hfill \cr 0 \hfill \cr} \right.\left. \matrix{ 0 \hfill \cr {a \over 2} \hfill \cr} \right|} \right) \cr&= \left( {{{{a^2}} \over 4};{a^2};{{{a^2}} \over 2}} \right) \cr & \Rightarrow {V_{A’CMN}} = {1 \over 6}\left| {{{{a^3}} \over 4} + {a^3} - {{{a^3}} \over 2}} \right| = {1 \over 6}\left| {{{3{a^3}} \over 4}} \right| = {{{a^3}} \over 8}. \cr} \)
