Cho tam giác đều ABC cạnh a và (P) là mặt phẳng qua BC và vuông góc với mặt phẳng (ABC). Gọi (C ) là đường tròn đường kính BC và nằm tròn mp(P).
1) Tính bán kính mặt cầu đi qua đường tròn (C ) và điểm A.
2) Xét hình nón ngoại tiếp mặt cầu nói trên sao cho các tiếp điểm giữa hình nón và mặt cầu là đường tròn (C ). Tính thể tích của khối nón.

1) 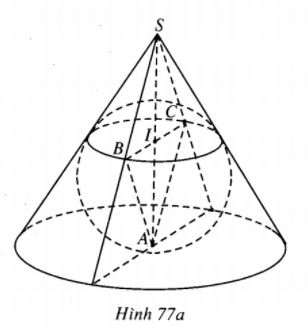
Gọi I là trung điểm của BC thì \(AI \bot BC.\) Do (P) là mặt phẳng chứa BC và vuông góc với mp(ABC) nên \(AI \bot (P).\)
Advertisements (Quảng cáo)
Mặt cầu chứa đường tròn (C ) và di qua điểm A có tâm trùng với tâm của đường tròn ngoại tiếp tam giác ABC, có bán kính bằng bán kính của đường tròn này. Vậy bán kính mặt cầu là
\(R = {{a\sqrt 3 } \over 3}.\)
2)
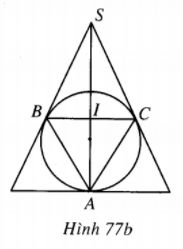
Hình nón thỏa mãn các giả thiết đã nêu tiếp xúc với mặt cầu tại điểm A và đỉnh S của hình nón thuộc đường thẳng AI. Dễ thấy mp(ABC) cắt mặt cầu theo đường tròn lớn và cắt hình nón theo tam giác cân có cạnh đáy đi qua A và tam giác cân này ngoại tiếp đường tròn lớn đó. Vì tam giác ABC đều nên dễ thấy tam giác cân nói trên cũng đều, từ đó cạnh của tam giác này bằng 2a, vậy đường cao của hình nón là \(SA = a\sqrt 3 \). Khi ấy thể tích khối nón phải tìm là
\(V = {1 \over 3}\pi {a^2}.a\sqrt 3 = {{\pi {a^3}\sqrt 3 } \over 3}.\)
