1) Tìm hình nón có thể tích lớn nhất nội tiếp một mặt cầu bán kính R cho trước.
2) Tìm hình nón có thể tích nhỏ nhất ngoại tiếp mặt cầu bán kính r cho trước.

1)
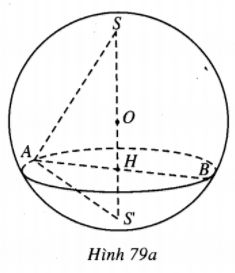
Kí hiệu bán kính đáy hình nón là x, chiều cao hình nón là y \((0 < x \le R,0 < y < 2R).\) Gọi SS’ là đường kính của mặt cầu ngoại tiếp hình nón ta có
\({x^2} = y\left( {2R - y} \right).\)
Gọi V1 là thể tích khối nón thì
\(\eqalign{ & {V_1} = {1 \over 3}\pi {x^2}y = {1 \over 3}\pi y.y(2R - y) \cr & = {\pi \over 6}\left( {4R - 2y} \right).y.y \cr & \le {\pi \over 6}{\left( {{{4R - 2y + y + y} \over 3}} \right)^3} = {{32\pi {R^3}} \over {81}}. \cr} \)
Vậy thể tích \({V_1}\) đạt giá trị lớn nhất bằng \({{32\pi {R^3}} \over {81}}\) khi và chỉ khi 4R-2y=y
\( \Leftrightarrow y = {{4R} \over 3},\) từ đó \({x^2} = {{4R} \over 3}\left( {2R - {{4R} \over 3}} \right) = {{8{R^2}} \over 9}\) hay \(x = {{2R\sqrt 2 } \over 3}.\)
2)
Advertisements (Quảng cáo)
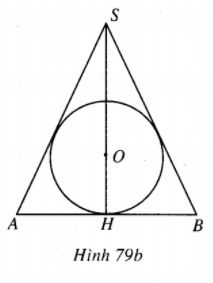
Xét mặt phẳng chứa trục của hình nón, mặt phẳng này cắt hình nón theo tam giác cân SAB và cắt mặt cầu nội tiếp hình nón theo đường tròn bán kính r và hình tròn này nội tiếp tam giác cân SAB (H.79b)
Kí hiệu bán kính đáy hình nón là x, chiều cao hình nón là y (x > 0, y > 2r) thì
\(\left( {AH + SA} \right)r = {1 \over 2}AB.SH\)
\( \Leftrightarrow (x + \sqrt {{x^2} + {y^2}} )r = xy \Leftrightarrow {x^2} = {{{r^2}y} \over {y - 2r}},\)
Vậy thể tích hình nón ngoại tiếp mặt cầu bán kính r là
\({V_2} = {1 \over 3}\pi {x^2}y = {1 \over 3}\pi {r^2}.{{{y^2}} \over {y - 2r}}.\)
Ta có
\(\eqalign{ & {{{y^2}} \over {y - 2r}} = {{{y^2} - 4{r^2} + 4{r^2}} \over {y - 2r}} = y + 2r + {{4{r^2}} \over {y - 2r}} \cr & = y - 2r + {{4{r^2}} \over {y - 2r}} + 4r \cr & \ge 2\sqrt {(y - 2r).{{4{r^2}} \over {y - 2r}}} + 4r = 8r. \cr} \)
Từ đó \({V_2} \ge {1 \over 3}\pi .8{r^3},\) tức là \({V_2}\) đạt giá trị bé nhất khi và chỉ khi
\(y - 2r = {{4{r^2}} \over {y - 2r}} \Leftrightarrow y = 4r,\)
Từ đó \(x = r\sqrt 2 .\)
