Tìm cực trị của các hàm số sau:a) \(y = 2{x^3} + 3{x^2}-36x + 1\)b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\)c) \(y = \sqrt { - {x^2} + 4} \)
Tìm tập xác định, đạo hàm và lập bảng biến thiên
a) \(y = 2{x^3} + 3{x^2}-36x + 1\)
Tập xác định: \(D = \mathbb{R}\)
\(y’ = 6{x^2} + 6x - 36\)
\(y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 3\end{array} \right.\)
Bảng biến thiên:
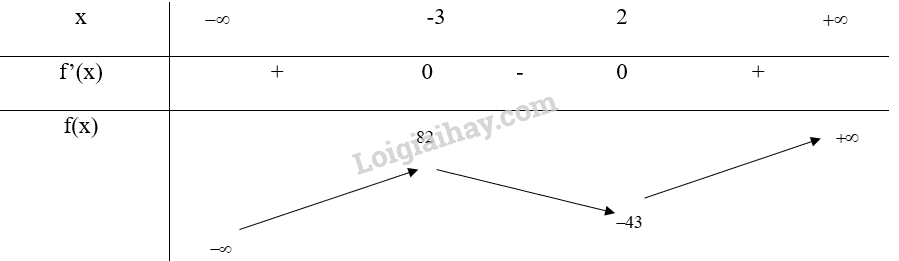
Hàm số đạt cực đại tại x = -3, \({y_{cd}} = f( - 3) = 82\), đạt cực tiểu tại x = 2, \({y_{ct}} = f(2) = - 43\)
b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 2\} \)
\(y’ = \frac{{{x^2} - 4x + 6}}{{{{(x - 2)}^2}}}\)
Ta có: \(\left\{ \begin{array}{l}({x^2} - 4x + 6) > 0\forall x \in \mathbb{R}\backslash \{ 2\} \\{(x - 2)^2} > 0\forall x \in \mathbb{R}\backslash \{ 2\} \end{array} \right.\) nên \(y’ > 0\forall x \in \mathbb{R}\backslash \{ 2\} \)
Bảng biến thiên:
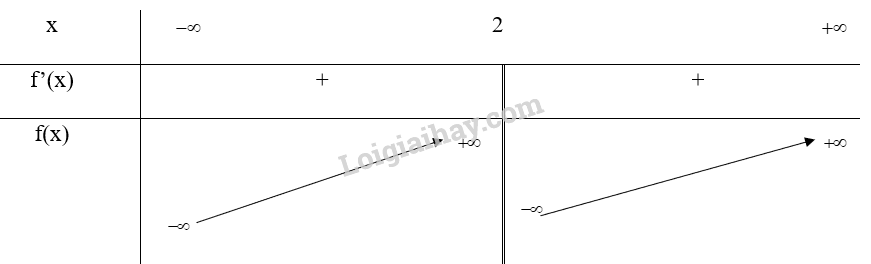
Vậy hàm số không có điểm cực trị
c) \(y = \sqrt { - {x^2} + 4} \)
Tập xác định: \(D = \left( { - 2;2} \right)\)
\(y’ = \frac{{ - x}}{{\sqrt { - {x^2} + 4} }}\)
\(y’ = 0 \Leftrightarrow x = 0\)
Bảng biến thiên:
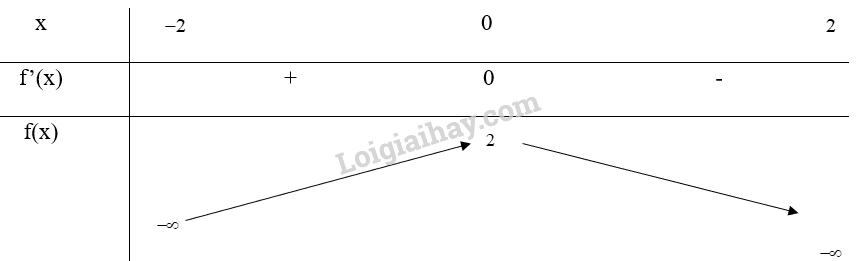
Hàm số đạt cực đại tại x = 0, \({y_{cd}} = f(0) = 2\)