
Xét một chất điểm chuyển động dọc theo trục \(Ox\). Toạ độ của chất điểm tại thời điểm \(t\) được xác định bởi hàm số \(x(t) = {t^3} - 6{t^2} + 9t\) với \(t \ge 0\). Khi đó \(x'(t)\) là vận tốc của chất điểm tại thời điểm \(t\), kí hiệu \(v(t)\); \(v'(t)\) là gia tốc chuyển động của chất điểm tại thời điểm \(t\), kí hiệu \(a(t)\). a) Tìm các hàm \(v(t)\)và \(a(t)\)b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?

Áp dụng công thức tính đạo hàm, xét dấu đạo hàm

a) \(v(t) = x'(t) = 3{t^2} - 12t + 9\)
Advertisements (Quảng cáo)
\(a(t) = v'(t) = 6t - 12\)
b) Tập xác định: \(D = [0; + \infty ]\)
\(a(t) = 0 \Leftrightarrow t = 2\)
Bảng biến thiên:
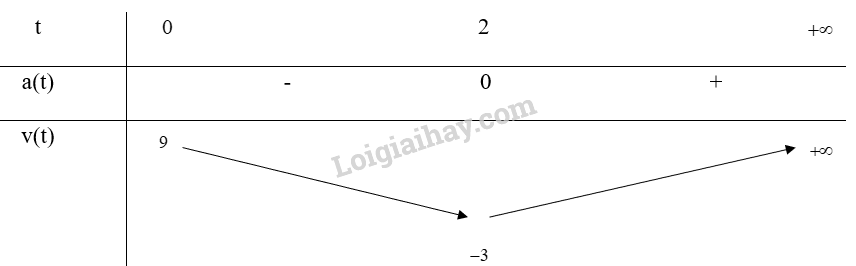
Vậy trong khoảng từ t = 0 đến t = 2 thì vận tốc của chất điểm giảm, từ t = 2 trở đi thì vận tốc của chất điểm tăng
