
Hộp sữa \(1l\) được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.

Tìm mối liên hệ giữa chiều cao và cạnh đáy, từ đó lập hàm số biểu diễn diện tích toàn phần của hộp theo x. Sau đó tìm đạo hàm, lập bảng biến thiên và xác định giá trị nhỏ nhất

Gọi chiều cao của hộp là h (cm)
Thể tích của hộp là: \(V = h.{x^2} = 1 \Leftrightarrow h = \frac{1}{{{x^2}}}\)
Advertisements (Quảng cáo)
Diện tích toàn phần của hộp là: \(y = {S_{tp}} = {S_{xq}} + {S_{day}} = 4hx + 2{x^2} = 4.\frac{1}{{{x^2}}}.x + 2{x^2} = 2{x^2} + \frac{4}{x}\)
Tập xác định: \(D = (0; + \infty )\)
\(y’ = 4x - \frac{4}{{{x^2}}} = 0 \Leftrightarrow x = 1\)
Bảng biến thiên:
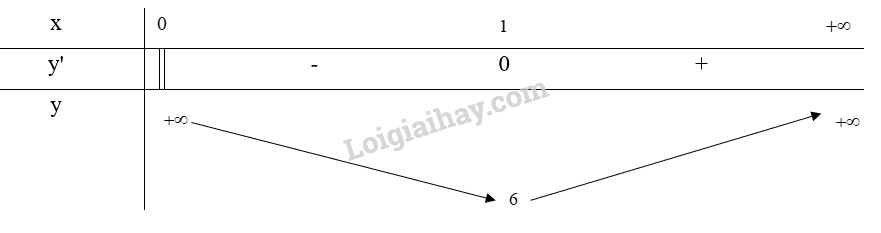
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_D y = y(1) = 6\)
Vậy x = 1cm thì diện tích toàn phần của hộp nhỏ nhất và bằng 6 \(c{m^2}\)
