Trả lời câu hỏi Khám phá 3 trang 60
Khám phá3
Trả lời câu hỏi Khám phá 3 trang 60
Cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm toạ độ của vectơ \(\overrightarrow {AB} \) theo toạ độ hai điểm A, B.

Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)

\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = ({x_A};{y_A};{z_A}) - ({x_B};{y_B};{z_B}) = ({x_A} - {x_B};{y_A} - {y_B};{z_A} - {z_B})\)
Thực hành3
Trả lời câu hỏi Thực hành 3 trang 61
Cho ba điểm M(7; –2; 0), N(–9; 0; 4), P(0; –6; 5).
a) Tìm toạ độ của các vectơ \(\overrightarrow {MN} ,\overrightarrow {NP} ,\overrightarrow {MP} \)
b) Tính các độ dài MN, NP, MP.

a) Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)

a) \(\overrightarrow {MN} = ( - 9 - 7;0 - ( - 2);4 - 0) = ( - 16;2;4)\)
\(\overrightarrow {NP} = (0 - ( - 9); - 6 - 0;5 - 4) = (9; - 6;1)\)
\(\overrightarrow {MP} = (0 - 7; - 6 - ( - 2);5 - 0) = ( - 7; - 4;5)\)
b) \(MN = \sqrt {{{( - 16)}^2} + {2^2} + {4^2}} = 2\sqrt {69} \)
\(NP = \sqrt {{9^2} + {{( - 6)}^2} + {1^2}} = \sqrt {118} \)
\(MP = \sqrt {{{( - 7)}^2} + {{( - 4)}^2} + {5^2}} = 3\sqrt {10} \)
Khám phá4
Trả lời câu hỏi Khám phá 4 trang 61
Cho tam giác ABC có \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Gọi \(M({x_M};{y_M};{z_M})\) là trung điểm của đoạn thẳng AB và \(G({x_G};{y_G};{z_G})\) là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ \(\overrightarrow {OM} = \frac{1}{2}(\overrightarrow {OA} + \overrightarrow {OB} )\),\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )\), tìm toạ độ của các điểm M và G.

Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a + \overrightarrow b = ({a_1} + {b_1};{a_2} + {b_2};{a_3} + {b_3})\)

\(\overrightarrow {OA} + \overrightarrow {OB} = ({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B})\)
\(\overrightarrow {OM} = \frac{1}{2}({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B}) = (\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)=> \(M(\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = {x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}\)
\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} ) = \frac{1}{3}({x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}) = (\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)=> \(G(\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)
Thực hành4
Trả lời câu hỏi Thực hành 4 trang 62
Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(–3; –1; 0). Tìm toạ độ:
a) Các điểm M′, N′, P′ lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M′N′P′.

Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC

a) \(M'(\frac{{1 - 3}}{2};\frac{{2 - 1}}{2};\frac{3}{2})\) hay \(M'( - 1;\frac{1}{2};\frac{3}{2})\)
\(N'(\frac{{2 - 3}}{2};\frac{{1 - 1}}{2};\frac{3}{2})\) hay \(N'( - \frac{1}{2};0;\frac{3}{2})\).
\(P'(\frac{{2 + 1}}{2};\frac{{1 + 2}}{2};\frac{{3 + 3}}{2})\) hay \(P'(\frac{3}{2};\frac{3}{2};3)\)
b) \(G(\frac{{2 + 1 - 3}}{3};\frac{{1 + 2 - 1}}{3};\frac{{3 + 3 + 0}}{3})\) hay \(G(0;\frac{2}{3};1)\)
Vận dụng3
Trả lời câu hỏi Vận dụng 3 trang 62
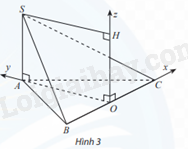
Cho hình chóp S.ABC có \(SA \bot (ABC)\), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy tìm toạ độ:
a) Các điểm A, S, B, C
Advertisements (Quảng cáo)
b) Trung điểm M của SB và trung điểm N của SC;
c) Trọng tâm G của tam giác SBC

\(\overrightarrow {OA} = (a;b;c) \Rightarrow A(a;b;c)\). Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC

a) \(OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - {{(\frac{a}{2})}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(\overrightarrow {OA} = \frac{{a\sqrt 3 }}{2}\overrightarrow j = (0;\frac{{a\sqrt 3 }}{2};0) \Rightarrow A(0;\frac{{a\sqrt 3 }}{2};0)\)
\(\overrightarrow {OB} = - \frac{a}{2}\overrightarrow i = ( - \frac{a}{2};0;0) \Rightarrow B( - \frac{a}{2};0;0)\)
\(\overrightarrow {OC} = \frac{a}{2}\overrightarrow i = (\frac{a}{2};0;0) \Rightarrow C(\frac{a}{2};0;0)\)
\(\overrightarrow {OS} = \frac{{a\sqrt 3 }}{2}\overrightarrow j + a\overrightarrow k = (0;\frac{{a\sqrt 3 }}{2};a) \Rightarrow S(0;\frac{{a\sqrt 3 }}{2};a)\)
b) \(M(\frac{{0 - \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(M( - \frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
\(N(\frac{{0 + \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(N(\frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
c) \(G(\frac{{0 + \frac{a}{2} - \frac{a}{2}}}{3};\frac{{\frac{{a\sqrt 3 }}{2}}}{3};\frac{a}{3})\) hay \(G(0;\frac{{a\sqrt 3 }}{6};\frac{a}{3})\)
Thực hành5
Trả lời câu hỏi Thực hành 5 trang 63
Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).
a) Tìm toạ độ điểm K là chân đường cao kẻ từ M của tam giác MNP.
b) Tìm độ dài cạnh MN và MP.
c) Tính góc M

a)\(\overrightarrow a \bot \overrightarrow b \Rightarrow \overrightarrow a .\overrightarrow b = 0\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
c) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)

a) Ta có: \(\overrightarrow {NP} = (2; - 1; - 1)\)
Gọi K(x;y;z) là chân đường cao kẻ từ M của tam giác MNP
=> \(\overrightarrow {NK} = (x - 5;y - 9;z - 3)\)
\(\overrightarrow {NK} \) cùng phương với \(\overrightarrow {NP} \) nên \(x - 5 = 2t;y - 9 = - t;z - 3 = - t\) => \(K(2t + 2; - t + 9; - t + 3)\)
Ta có: \(\overrightarrow {MK} = (2t + 2; - t + 8; - t + 1)\)
\(\overrightarrow {MK} \bot \overrightarrow {NP} \Leftrightarrow \overrightarrow {MK} .\overrightarrow {NP} = 0 \Leftrightarrow (2t + 2).2 - ( - t + 8) - ( - t + 1) = 0 \Leftrightarrow t = \frac{5}{6}\)
Vậy \(K(\frac{{11}}{3};\frac{{49}}{6};\frac{{13}}{6})\)
b) Ta có: \(\overrightarrow {MN} = (5;8;1) \Rightarrow MN = \sqrt {{5^2} + {8^2} + {1^2}} = 3\sqrt {10} \)
\(\overrightarrow {MP} = (7;7;0) \Rightarrow MP = \sqrt {{7^2} + {7^2}} = 7\sqrt 2 \)
c) \(\cos M = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{|\overrightarrow {MN} |.|\overrightarrow {MP} |}} = \frac{{5.7 + 8.7}}{{3\sqrt {10} .7\sqrt 2 }} = \frac{{13\sqrt 5 }}{{30}}\)
Vận dụng4
Trả lời câu hỏi Vận dụng 4 trang 64
Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có toạ độ là A(1; 1; 1), B(5; 7; 9), C(9; 11 ; 4). Tính:
a) Các khoảng cách giữa mỗi cặp drone giao hàng.
b) Góc \(\widehat {BAC}\)

a) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
b) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)

a) \(\overrightarrow {AB} = (4;6;8) \Rightarrow AB = \sqrt {{4^2} + {6^2} + {8^2}} = 2\sqrt {29} \)
\(\overrightarrow {AC} = (8;10;3) \Rightarrow \sqrt {{8^2} + {{10}^2} + {3^2}} = \sqrt {173} \)
\(\overrightarrow {BC} = (4;4; - 5) \Rightarrow \sqrt {{4^2} + {4^2} + {{( - 5)}^2}} = \sqrt {57} \)
c) \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{|\overrightarrow {AB} |.|\overrightarrow {AC} |}} = \frac{{4.8 + 6.10 + 8.3}}{{2\sqrt {29} .\sqrt {173} }} \approx 0,82 \Rightarrow \widehat {BAC} = 35,03^\circ \)
