Bài 11 trang 118 Tài liệu dạy học Toán lớp 6 tập 2:  ...

Cho hai góc kề bù $\widehat {AOB}$ và $\widehat {AOC}$. Biết $\widehat {AOB} = {124^o}$

a) Tính $\widehat {AOC}$.

b) Trên cùng nửa mặt phẳng bờ BC, chứa tia OA, vẽ $\widehat {COD} = {118^o}$. Tia OD có là tia phân giác của $\widehat {AOB}$ không ? Vì sao ?

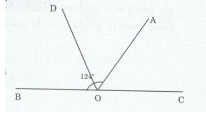
a)Hai góc AOB và AOC kề bù nên $\widehat {AOB} + \widehat {AOC} = {180^0}.$

Do đó: $\widehat {AOC} = {180^0} - \widehat {AOB} = {180^0} - {124^0} = {56^0}.$

b) Hai góc COD và BOD kề bù.

Nên $\widehat {COD} + \widehat {BOD} = {180^0}.$

Do đó: $\widehat {BOD} = {180^0} - \widehat {COD} = {180^0} - {118^0} = {62^0}.$

Hai tia OA và OD cùng thuộc một nửa mặt phẳng bờ BC, $\widehat {BOD} < \widehat {BOA}({62^0} < {124^0}).$

Nên tia OD nằm ở giữa hai tia OB, OA.

Do đó: $\widehat {BOD} + \widehat {DOA} = \widehat {BOA}$

$\Rightarrow \widehat {DOA} = \widehat {BOA} - \widehat {BOD}$$\, = {124^0} - {62^0} = {62^0}.$

Vậy $\widehat {BOD} = \widehat {AOD} = {{\widehat {BOA}} \over 2}( = {62^0}).$

Mà tia OD nằm giữa hai tia OA và OB. Nên tia OD là tia phân giác của góc AOB. Đường thẳng m chia mặt phẳng thành hai nửa mặt phẳng bờ m nên A nằm trong một nửa mặt phẳng bờ m chứa điểm A.