Bài 12 trang 118 Tài liệu dạy – học toán 6 tập 2. . Bài: Ôn tập chương 2
Cho góc bẹt aOb, vẽ tia Ot là phân giác của \(\widehat {aOb}\), Om là phân giác của \(\widehat {aOt}\), On là phân giác của \(\widehat {tOb}\). Chứng tỏ \(\widehat {mOn}\) vuông.
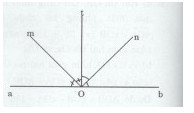
Ta có: \(\widehat {aOt} + \widehat {bOt} = {180^0}\) (kề bù)
Advertisements (Quảng cáo)
Mà \(\widehat {mOt} = {1 \over 2}\widehat {aOt}\) (Om là tia phân giác của góc aOt)
Và \(\widehat {nOt} = {1 \over 2}\widehat {bOt}\) (On là phân giác của góc bOt)
Và \(\widehat {mOn} = \widehat {mOt} + \widehat {nOt}\) (tia Ot nằm giữa hai tia Om và On)
Do đó: \(\widehat {mOn} = \widehat {mOt} + \widehat {nOt} = {1 \over 2}\widehat {aOt} + {1 \over 2}\widehat {bOt} = {1 \over 2}(\widehat {aOt} + \widehat {bOt}) = {1 \over 2}{.180^0} = {90^0}.\)