
Cho tam giác nhọn ABC và trực tâm H. Em hãy xác định trực tâm của các tam giác BCH, CHA, HAB.

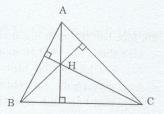
Ta có H là trực tâm của tam giác ABC (gt)
Nên \(CH \bot AB,BH \bot AC\) và \(AH \bot BC\)
∆BHC có: BA là đường cao (\(BA \bot CH\))
CA là đường cao (\(CA \bot BH\))
DA là đường cao (\(DA \bot BC\)) và BA, CA, DA cắt nhau tại A
Do đó A là trực tâm của ∆BHC
∆AHC có: BA là đường cao \((CH \bot AB)\)
Advertisements (Quảng cáo)
BF là đường cao \((BF \bot AC)\)
BC là đường cao \((BC \bot AH)\)
BA, BF, BC cắt nhau tại B
Do đó B là trực tâm của ∆AHC.
∆ABH có: CA là đường cao \((CA \bot BH)\)
CE là đường cao \((CE \bot AB)\)
CB là đường cao \((CB \bot AH)\)
CA, CE, CB cắt nhau tại C
Do đó C là trực tâm của ∆ABH.
