Bài tập - Chủ đề 6 : Các đường đồng quy của tam giác - Bài tập 26 trang 123 Tài liệu dạy – học Toán 7 tập 2. Giải bài tập Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.

Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.

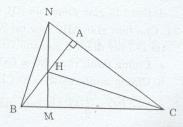
Xét ∆NBC có:
BA là đường cao \((BA \bot AC,N \in CA)\)
Advertisements (Quảng cáo)
NM là đường cao \((HM \bot BC,N \in MH)\)
Và BA cắt NM tại H (gt)
Do đó H là trực tâm của ∆NBC
=> CH là đường cao của ∆NBC
Vậy \(CH \bot NB.\)
