
Cho tam giác ABC vuông tại A, BD là phân giác của góc ABC (D thuộc AC).
Trên nửa mặt phẳng bờ AC không chứa điểm B, qua điểm C vẽ tia Cx vuông góc với CA và cắt tia BD tại E. Chứng minh chu vi tam giác ADB nhỏ hơn chu vi tam giác CDE.

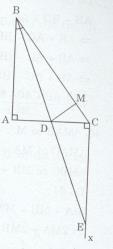
∆ABC vuông tại A. Ta có \(AB \bot AC\) tại A => AB < BC
Trên cạnh BC lấy điểm M sao cho BM = AB
Xét ∆MBD và ∆ABD có: \(\widehat {MBD} = \widehat {ABD}\) (BD là đường phân giác)
MB = AB
BD (cạnh chung)
Do đó ∆MBD = ∆ABD (c.g.c) \( \Rightarrow \widehat {BMD} = \widehat {BAD} = 90^\circ ,AD = MD\)
\(DM \bot BC\) tại M => DM < CD. Nên AD < CD
Advertisements (Quảng cáo)
Mặt khác
\(AB \bot AC,EC \bot AC\)
\( \Rightarrow AB//EC \Rightarrow \widehat {CEB} = \widehat {ABD}\) (so le trong)
Ta có \(\widehat {CEB} = \widehat {MBD}( = \widehat {ABD)}\) => ∆CBE cân tại C => BC = CE
Nên AB < BC = CE
∆ABD vuông tại A => BD2 = AD2 + AB2 (định lí Pythagore)
∆CDE vuông tại E => DE2 = CD2 + CE2
Mà AD < CD và AB < CE. Do đó
BD2 < DE2 => BD < DE
Ta có AD + AB + BD < CD + CE + DE
Vậy chu vi tam giác ADB nhỏ hơn chu vi tam giác CDE.
