
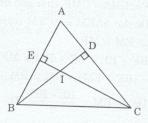
Cho tam giác ABC nhọn (AB < AC). Kẻ \(BD \bot AC\,\,\left( {D \in AC} \right)\) và \(CE \bot AB\,\,\left( {E \in AB} \right)\) . Đoạn thẳng BD cắt CE tại I.
a) SO sánh \(\widehat {ABD}\) và \(\widehat {ACE}\)
b) Chứng minh IB < IC
c) Chứng minh CE > BD.

a) Ta có \(\widehat {ABD} + \widehat A = 90^\circ\) (∆ABD vuông tại D)
\(\widehat {ACE} + \widehat A = 90^\circ\) (∆ACE vuông tại E)
Advertisements (Quảng cáo)
Do đó \(\widehat {ABD} = \widehat {ACE}\)
b) ∆ABC có AB < AC (gt) \( \Rightarrow \widehat {ACB} < \widehat {ABC}\) (quan hệ giữa cạnh và góc trong một tam giác)
\( \Rightarrow \widehat {ACE} + \widehat {ICB} < \widehat {ABE} + \widehat {IBC}\)
Do đó \(\widehat {ICB} < \widehat {IBC}\)
∆IBC có \(\widehat {ICB} < \widehat {IBC} \Rightarrow IB < IC\)
c) \({S_{ABC}} = {1 \over 2}CE.AB,{S_{ABC}} = {1 \over 2}BD.AC \Rightarrow {1 \over 2}CE.AB = {1 \over 2}BD.AC\)
Mà AB < AC (gt). Do đó CE > BD.
