Advertisements (Quảng cáo)
Tam giác ABC cân tại A, trên cạnh BC lấy các điểm D, E sao cho BD = DE = EC. Chứng minh rằng trong ba góc BAD, DAE, EAC thì góc DAE là góc lớn nhất.
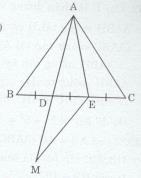
Xét ∆ABD và ∆ACE có: AB = AC (∆ABC cân tại A)
\(\widehat {ABD} = \widehat {ACE}\) (∆ABC cân tại A)
BD = EC (gt)
Do đó ∆ABD = ∆ACE (c.g.c) \( \Rightarrow \widehat {BAD} = \widehat {EAC}\)
Ta có \(\widehat {AEB} > \widehat C(\widehat {AEB}\) là góc ngoài của tam giác ACD)
\(\widehat C = \widehat B\) (∆ABC cân tại A)
Advertisements (Quảng cáo)
Nên \(\widehat {AEB} > \widehat B\)
∆ABE có \(\widehat {AEB} > \widehat B\) => AB > AE
Trên tia đối của tia DA lấy điểm M sao cho DM = DA
Xét ∆DME và ∆DAB có DM = DA, \(\widehat {MDE} = \widehat {ADB}\) (đối đỉnh), DE = BD (gt)
Do đó ∆DME = ∆DAB (c.g.c) \( \Rightarrow ME = AB,\widehat {DME} = \widehat {BAD}\)
Ta có ME > AE. ∆AEM có ME > AE \( \Rightarrow \widehat {DAE} > \widehat {DME}\)
Nên \(\widehat {DAE} > \widehat {BAD} = \widehat {EAC}.\)
Vậy trong ba góc BAD, DAE, EAC thì góc DAE lớn nhất.